题目内容
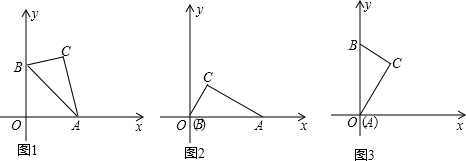
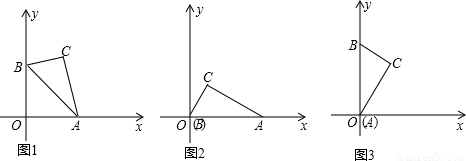
如图1,有一块30°、60°、90°的三角板所对应的点为A、B、C,斜边AB为4个单位长度,且A、B两点分别在x轴、y轴上滑动,记∠BAO=α.(当B点与O点重合时,记α=0°,如图2所示;当A点与O点重合时,记α=90°,如图3所示).

(1)当α=0°时,直接写出点C的坐标______;当α=90°时,直接写出点C的坐标______;
(2)当α=60°时,直接写出点C的坐标______;
(3)请从α=15°、α=30°、α=45°、α=75°中任意选两个角度,分别求出点C的坐标;(其中一个写出详细的求解过程,另一个直接写出答案)当α=______时,点C的坐标为______;
(4)根据前面的探索,当α为任意锐角时,你认为点C是否会落在某条线段上运动,若存在,请写出这条线段所在直线的函数表达式及自变量的取值范围;若不存在,请说明理由.(参考数据:sin15°=cos75°= ,sin75°=cos15°=
,sin75°=cos15°=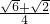 )
)
解:(1)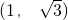 ;
; ;
;
(2)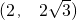 ;
;
(3)当α=15°时,过C作CD⊥x轴于点D,
在Rt△ABC中,AB=4,∠BAC=30°,∴ .
.
在Rt△ACD中, ,∠DAC=45°,∴
,∠DAC=45°,∴ .
.
在Rt△AOB中,AB=4,∠BAO=15°,
∴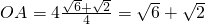 .
.
∴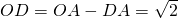 .∴
.∴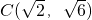 ;
;
同理:当α=30°时,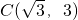 ;
;
当α=45°时, ;
;
当α=75°时,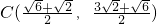 ;
;
(4)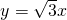
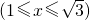 .
.
分析:根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长.
点评:本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.
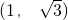 ;
; ;
;(2)
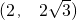 ;
;(3)当α=15°时,过C作CD⊥x轴于点D,
在Rt△ABC中,AB=4,∠BAC=30°,∴
 .
.在Rt△ACD中,
 ,∠DAC=45°,∴
,∠DAC=45°,∴ .
.在Rt△AOB中,AB=4,∠BAO=15°,
∴
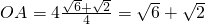 .
.∴
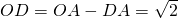 .∴
.∴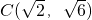 ;
;同理:当α=30°时,
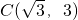 ;
;当α=45°时,
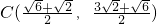 ;
;当α=75°时,
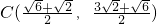 ;
;(4)
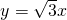
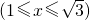 .
.分析:根据题中所给的条件,在直角三角形中解题,根据角的正弦值与三角形边的关系,可求出各边的长.
点评:本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目