题目内容
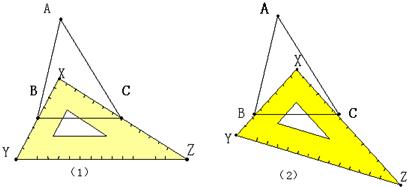
(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=______,∠XBC+∠XCB=______.
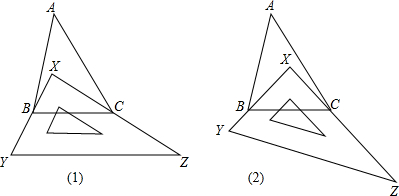
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.
解:(1)∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABC+∠ACB=150°;∠XBC+∠XCB=90°.
(2)不变化.
∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)
=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
分析:本题考查的是三角形内角和定理.已知∠A=30°易求∠ABC+∠ACB的度数.又因为x为90°,所以易求∠XBC+∠XCB.
点评:此题注意运用整体法计算.关键是求出∠ABC+∠ACB.
∴∠ABC+∠ACB=150°,
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABC+∠ACB=150°;∠XBC+∠XCB=90°.
(2)不变化.
∵∠A=30°,
∴∠ABC+∠ACB=150°,
∵∠X=90°,
∴∠XBC+∠XCB=90°,
∴∠ABX+∠ACX=(∠ABC-∠XBC)+(∠ACB-∠XCB)
=(∠ABC+∠ACB)-(∠XBC+∠XCB)=150°-90°=60°.
分析:本题考查的是三角形内角和定理.已知∠A=30°易求∠ABC+∠ACB的度数.又因为x为90°,所以易求∠XBC+∠XCB.
点评:此题注意运用整体法计算.关键是求出∠ABC+∠ACB.

练习册系列答案
相关题目
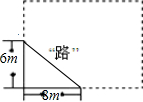 如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了
如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了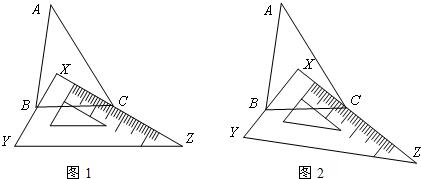
 23、如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
23、如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积. 如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将其阴影部分进行绿化,中间正方形部分将修建一座雕塑,正方形的边长是(a+b)米.
如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将其阴影部分进行绿化,中间正方形部分将修建一座雕塑,正方形的边长是(a+b)米.