题目内容
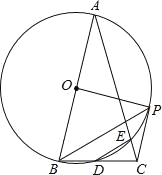
【题目】如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的阴影部分的面积是 ;
围成的阴影部分的面积是 ;
(2)求线段DE的长.
【答案】(1)9π+18;(2)DE=![]() +6;
+6;
【解析】
(1)根据题意作出合适的辅助线,然后根据题目中的数据和图形,即可求得阴影部分的面积;
(2)根据题意和图形,利用平行线的性质和特殊角的三角函数可以求得DE的长.
(1)如图,连接OD,
∵⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,
∴∠ADB=90°,AD=BD,
∴∠OBD=∠ODB=45°,
∴OB=OD=6,
∴由AB,BD,![]() 围成的阴影部分的面积是:
围成的阴影部分的面积是:![]() (
(![]()
![]() )=9π+18,
)=9π+18,
故答案为:9π+18;
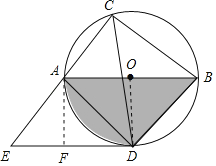
(2)如图,作AF⊥DE于点F,则AF=OD=6,
∵AB∥DE,∠OAD=45°,
∴∠ADF=∠OAD=45°,
∴DF=AF=6,
∵∠ACB=90°,AC=6,AB=12,
∴∠CBA=30°,
∴∠CAB=60°,
∵AB∥DE,
∴∠E=∠CAB=60°,
∵AF=6,∠AFE=90°,
∴EF=![]() =
=![]() =2
=2![]() ,
,
∴DE=EF+DF=2![]() +6.
+6.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】为让家园更美丽,我市今年进一步推进全国文明城市、 国家卫生城市的创建工作,学校把“双创”工作推向深入,组织了以文明卫生知识竞赛,每班派相同人数的学生参加,成绩分别为![]() 四个等级.其中相应等级的得分依次记为
四个等级.其中相应等级的得分依次记为![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图表:
分,学校将八年级的一班和二班的成绩整理并绘制成如下统计图表: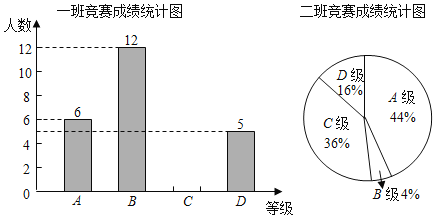
班级 | 平均数(分) | 中位数(分) | 众数(分) |
一班 |
|
|
|
二班 |
|
|
|
根据以上提供的信息解答下列问题:
(1)请补全一班竞赛成绩统计图;
(2)请直接写出![]() 的值;
的值;
(3)你认为哪个班成绩较好,诸写出支持你观点的理由.
【题目】某学校举行一场知识竞赛活动,竞赛共有4小题,每小题5分,答对给5分,答错或不答给0分,在该学校随机抽取若干同学参加比赛,成绩被制成不完整的统计表如下.
成绩 | 人数(频数) | 百分比(频率) |
0 | ||
5 | 0.2 | |
10 | 5 | |
15 | 0.4 | |
20 | 5 | 0.1 |
根据表中已有的信息,下列结论正确的是( )
A. 共有40名同学参加知识竞赛
B. 抽到的同学参加知识竞赛的平均成绩为10分
C. 已知该校共有800名学生,若都参加竞赛,得0分的估计有100人
D. 抽到同学参加知识竞赛成绩的中位数为15分