题目内容
【题目】用配方法解下列方程:
(1)x2-4x+1=0; (2)4x2+8x+1=0;
(3)2x2-x-1=0 (4)y2+2(![]() +1)y+2
+1)y+2![]() =0;
=0;
【答案】解:(1)x![]() =2+
=2+![]() ,x
,x![]() =2
=2![]() ;(2)x
;(2)x![]() =1+
=1+![]() ,x
,x![]() =1
=1![]() ;(3)x
;(3)x![]() =1,x
=1,x![]() =
=![]() ;(4)y
;(4)y![]() =1
=1![]() ,y
,y![]() =3
=3![]() .
.
【解析】
各方程二次项系数化为1,常数项移到右边,两边加上一次项系数一半的平方,利用完全平方公式变形后,再利用平方根定义开方即可求出解.
(1)方程移项得:x![]() 4x=1,
4x=1,
配方得:x![]() 4x+4=3,即(x2)
4x+4=3,即(x2) ![]() =3,
=3,
开方得:x2=±![]() ,
,
解得:x![]() =2+
=2+![]() ,x
,x![]() =2
=2![]() ;
;
(2)方程整理得:x![]() +2x=
+2x=![]() ,
,
配方得:![]() +2x+1=
+2x+1=![]() ,即(x+1)
,即(x+1) ![]() =
=![]() ,
,
开方得:x+1=±![]() ,
,
解得:x![]() =1+
=1+![]() ,x
,x![]() =1
=1![]() ;
;
(3)方程整理得:x![]()
![]() x=
x=![]() ,
,
配方得:x![]()
![]() x+
x+![]() =
=![]() ,即(x
,即(x![]() )
) ![]() =
=![]() ,
,
开方得:x![]() =±
=±![]() ,
,
解得:x![]() =1,x
=1,x![]() =
=![]() ;
;
(4)移项得:y![]() +2(
+2(![]() +1)y=2
+1)y=2![]() ,
,
配方得:y![]() +2(
+2(![]() +1)y+4+2
+1)y+4+2![]() =4,即(y+
=4,即(y+![]() +1)
+1) ![]() =4,
=4,
开方得:y+![]() +1=±2,
+1=±2,
解得:y![]() =1
=1![]() ,y
,y![]() =3
=3![]() .
.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】某校要从小明和小亮两名运动员中挑出一人参加立定跳远比赛,学校记录了二人在最近的6次立定跳远选拔赛中的成绩(单位:cm),并进行整理、描述和分析.下面给出了部分信息.
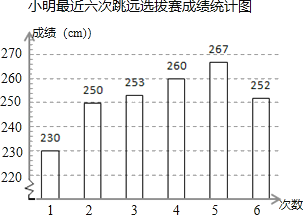
a.如图
b.小亮最近6次选拔赛成绩如下:
250 | 254 | 260 | 271 | 255 | 240 |
c.小明和小亮最近6次选拔赛中成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
小明 | 252 | 252.5 | 129.7 |
小亮 | 255 | m | 88.7 |
根据以上信息,回答下列问题:
(1)m= ;
(2)历届比赛表明:成绩达到266cm就有可能夺冠,成绩达到270cm就能打破纪录(积分加倍),根据这6次选拔赛成绩,你认为应选 (填“小明”或“小亮”)参加这项比赛,理由是 .(至少从两个不同的角度说明推断的合理性)
【题目】为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目).并将调查结果绘制成如下统计图表:
学生最喜欢的节目人数统计表
节目 | 人数(名) | 百分比 |
最强大脑 | 5 | 10% |
阅读者 | 15 | B% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
根据以上提供的信息,解答下列问题
(1)x= ,a= ,b= ;
(2)补全条形统计图;
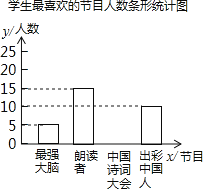
(3)若该校共有学生800名,根据抽样调查结果,估计该校喜爱《中国诗词大会》节目的学生有多少名?
(4)李玲和王亮经过选拔代表班级参加校内即将举办的“中国诗词大会”,预赛分为A、B、C三组进行,由抽签确定分组.李玲和王亮恰好分在一组的概率是多少?(要求用画树状图或列表法)