题目内容
【题目】如图,在平面直角坐标系中,A(﹣1,0),B(3,0),C(0,2),CD∥x轴,CD=AB.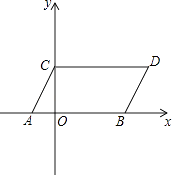
(1)求点D的坐标:
(2)四边形OCDB的面积S四边形OCDB;
(3)在 y轴上是否存在点P,使S△PAB=S四边形OCDB?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)解:∵点C的坐标为(0,2),A(﹣1,0),B(3,0),
则AB=4,
∴D点坐标为(4,2)
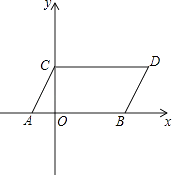
(2)解:∵CD∥BA,CD=AB
∴四边形ABDC为平行四边形,
∴四边形ABDC的面积=2×4=8,
∴S四边形OCDB=8﹣ ![]() ×1×2=7
×1×2=7
(3)解:存在.
设P点坐标为(0,t),
∵S△PAB=S四边形OCDB,
∴ ![]() 4|t|=7,
4|t|=7,
解得t=±3.5,
∴P点坐标为(0,3.5)或(0,﹣3.5)
【解析】
①根据点的平移规律得到D点坐标;
②根据平行四边形的面积公式-△AOC的面积=四边形OCDb的面积.
③设p点的坐标,再根据三角形面积公式求出t值,然后写出p点坐标.
【考点精析】掌握三角形的面积是解答本题的根本,需要知道三角形的面积=1/2×底×高.

练习册系列答案
相关题目
【题目】已知二次函数y=x2+bx+c中,函数y与自变量x的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 10 | 5 | 2 | 1 | 2 | 5 | … |
若A(m,y1),B(m+6,y2)两点都在该函数的图象上,当m=时,y1=y2 .
