题目内容
【题目】点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 和
和![]() ,抛物线
,抛物线![]() 的顶点在线段
的顶点在线段![]() 上运动时,形状保持不变,且与
上运动时,形状保持不变,且与![]() 轴交于
轴交于![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),给出下列结论:①
的左侧),给出下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 随
随![]() 的增大而增大;③若点
的增大而增大;③若点![]() 的横坐标最大值为
的横坐标最大值为![]() ,则点
,则点![]() 的横坐标最小值为
的横坐标最小值为![]() ;④当四边形
;④当四边形![]() 为平行四边形时,
为平行四边形时,![]() .其中正确的是( )
.其中正确的是( )
A. ②④ B. ②③ C. ①③④ D. ①②④
【答案】A
【解析】
根据顶点在线段AB上抛物线与y轴的交点坐标为(0,c)可以判断出c的取值范围,得到①错误;根据二次函数的增减性判断出②正确;先确定x=1时,点D的横坐标取得最大值,然后根据二次函数的对称性求出此时点C的横坐标,即可判断③错误;令y=0,利用根与系数的关系与顶点的纵坐标求出CD的长度的表达式,然后根据平行四边形的对边平行且相等可得AB=CD,然后列出方程求出a的值,判断出④正确.
∵ 点 A ,B 的坐标分别为 (2,3) 和 (1,3) ,
∴ 线段 AB 与 y 轴的交点坐标为 (0,3) ,
又 ∵ 抛物线的顶点在线段 AB 上运动,抛物线与 y 轴的交点坐标为 (0,c) ,
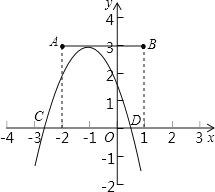
∴c≤3 , ( 顶点在 y 轴上时取“ = ” ) ,故①错误;
∵ 抛物线的顶点在线段 AB 上运动,
∴ 当 x<2 时, y 随 x 的增大而增大,
因此,当 x<3 时, y 随 x 的增大而增大,故②正确;
若点 D 的横坐标最大值为 5 ,则此时对称轴为直线 x=1 ,
根据二次函数的对称性,点 C 的横坐标最小值为 24=6 ,故③错误;
令 y=0 ,则 ax2+bx+c=0 ,
CD2=(![]() )24×
)24×![]() =
=![]() ,
,
根据顶点坐标公式,![]() ,
,
∴![]() =12 ,
=12 ,
∴CD2=![]() ×(12)=
×(12)= ![]() ,
,
∵ 四边形 ACDB 为平行四边形,
∴CD=AB=1(2)=3,
∴![]() =32=9 ,
=32=9 ,
解得 a=![]() ,故④正确;
,故④正确;
综上所述,正确的结论有②④.
故选A.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案