题目内容
【题目】如图,在菱形ABCD中,∠BAD=60°,点M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是9,则AB的长是( ) 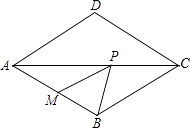
A.6 ![]()
B.3 ![]()
C.9
D.4.5
【答案】A
【解析】解:如图所示,连接DP,则根据菱形的对角线互相垂直平分,可得PD=BP, 当点M,P,D三点共线时,BP+MP=DP+MP=DM=9(最短),
连接BD,根据∠BAD=60°,可得△ABD是等边三角形,
∵点M是AB的中点,
∴DM⊥AB,
∴∠ADM=30°,
∵AM= ![]() =3
=3 ![]() ,
,
∴AD=2AM=6 ![]() ,
,
∴AB=6 ![]() ,
,
故选:A.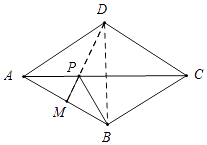
【考点精析】根据题目的已知条件,利用菱形的性质的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

练习册系列答案
相关题目