题目内容
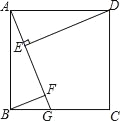
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F.
(1)如图1,求证:AE=BF;
(2)连接DF,若tan∠BAG=![]() ,AB=2
,AB=2![]() ,求△ADF的面积.
,求△ADF的面积.
【答案】(1)见解析;(2)8.
【解析】
(1)利用正方形的性质证明△BAF和△ADE全等.(2)利用(1)和已知条件,分别求出DE,AF长就可以求出三角形面积,
(1)∵四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE,
∴∠AB=AD,∠BAD=90°,∠AED=90°,∠AED=∠BFA,
∴∠BAF+∠EAD=90°,∠EAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△BAF和△ADE中,
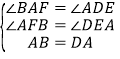 ,
,
∴△BAF≌△ADE(AAS),
∴BF=AE,
即AE=BF;
(2)由(1)知∠AED=∠BFA=90°,
∵tan∠BAG=![]() ,AB=2
,AB=2![]() ,
,
∴tan∠BAF=![]() ,
,
∴AF=4,BF=2,
由(1)知,△BAF≌△ADE,
∴AF=DE,
∴DE=4,
∵∠AED=90°,
∴△ADF的面积是:![]()

练习册系列答案
相关题目