题目内容
在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠C=60°,点E、F是AD、CD上两点,且DE=CF,AF、BE交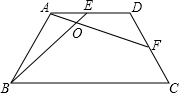 于点O.
于点O.
(1)请你猜测∠BOF=
(2)试证明你所猜测的结果.
 于点O.
于点O.(1)请你猜测∠BOF=
120°
120°
.(2)试证明你所猜测的结果.
分析:(1)根据题中所给条件可知∠BOF=120°;
(2)通过SAS证明△ABE≌△DAF,可知∠BOF=∠ABO+∠OAB=∠DAF+∠OAB=∠EAB,又∠C=60°,可知∠EAB=120°,继而即可求出的答案.
(2)通过SAS证明△ABE≌△DAF,可知∠BOF=∠ABO+∠OAB=∠DAF+∠OAB=∠EAB,又∠C=60°,可知∠EAB=120°,继而即可求出的答案.
解答:解:(1)∠猜测BOF=120°;
(2)∵四边形ABCD为等腰梯形,∠C=60°,
又∵AD=CD=AB,DE=CF,
∴AE=DF,
在△ABE和△DAF中,
,
∴△ABE≌△DAF,
∴∠BOF=∠ABO+∠OAB=∠DAF+∠OAB=∠EAB,
又∵∠EAB=120°,
∴∠BOF=120°.
(2)∵四边形ABCD为等腰梯形,∠C=60°,
又∵AD=CD=AB,DE=CF,
∴AE=DF,
在△ABE和△DAF中,
|
∴△ABE≌△DAF,
∴∠BOF=∠ABO+∠OAB=∠DAF+∠OAB=∠EAB,
又∵∠EAB=120°,
∴∠BOF=120°.
点评:本题考查等腰梯形的性质及全等三角形的判定与性质,难度适中,解题关键是找出关系∠BDF=∠ABO+∠OAB=∠DAF+∠OAB=∠EAB.

练习册系列答案
相关题目
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.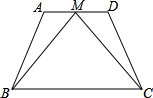 如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么?
如图,在等腰梯形ABCD中,AD∥BC,M是AD的中点,MB=MC吗?为什么? 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.