题目内容
如图,已知O是正方形ABCD对角线AC上一点,以O为圆心,OA的长为半径的圆O与BC相切于M,与AB、AD分别相交于E、F.(1)求证:CD与⊙O相切;(2)若正方形ABCD的边长为1,求⊙O的半径:(3)对于以点M、E、A、F以及CD与⊙O的切点N为顶点五边形的五条边,从相等关系考虑,你可以得出什么结论?请给出证明.

答案:
解析:
解析:
|
(1)连接OM,则OM⊥BC.过O作ON⊥CD于N.∵点O在正方形ABCD的对角线AC上,∠ACB=∠ACD= (2)设⊙O的半径为R,则OM=R, ∵正方形ABCD的边长为1,AC= 在Rt△OMC中,sin∠OCM= (3)对于五边形MEAFN的五条边,从相等关系考虑,有①AE=AF=MN;②EM=FN. |

练习册系列答案
相关题目
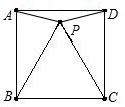 如图,已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径为a,则正方形ABCD边长为(
如图,已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径为a,则正方形ABCD边长为(A、
| ||||
B、
| ||||
| C、a | ||||
D、
|
 15、如图,已知P是正方形ABCD内一点,要使△APD≌△BPC,只需增加的一个条件是
15、如图,已知P是正方形ABCD内一点,要使△APD≌△BPC,只需增加的一个条件是 如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点.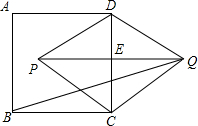 如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为
如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为 如图,已知E是正方形ABCD的边CD的中点,点F在边CD上,且∠BAE=∠FAE,
如图,已知E是正方形ABCD的边CD的中点,点F在边CD上,且∠BAE=∠FAE,