题目内容
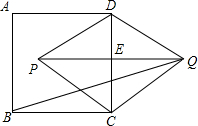 如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为
如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为分析:先作辅助线,因为ABCD是正方形,CD为等边△PCD和等边△QCD公共边,所以CD=CP=PD=CQ=QD,DE=CE,QE=EP.
tan∠PQB=
.
tan∠PQB=
| FB |
| FQ |
解答: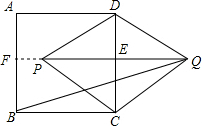 解:如图,延长QP交AB于F
解:如图,延长QP交AB于F
∵ABCD是正方形,三角形PCD和三角形QCD是以CD为边的等边三角形,
∴四边形PCQD是菱形,
设正方形的边长为a,则可得PE=QE=
a,DE=EC=
a,
∴tan∠BQF=
=
=2-
.
故答案为:2-
.
 解:如图,延长QP交AB于F
解:如图,延长QP交AB于F∵ABCD是正方形,三角形PCD和三角形QCD是以CD为边的等边三角形,
∴四边形PCQD是菱形,
设正方形的边长为a,则可得PE=QE=
| ||
| 2 |
| 1 |
| 2 |
∴tan∠BQF=
| FB |
| FQ |
| ||||
a+
|
| 3 |
故答案为:2-
| 3 |
点评:主要考查矩形和等边三角形边长相等及直角三角形三角函数的性质.

练习册系列答案
相关题目
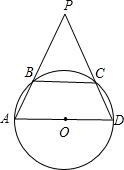 如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )
如图,已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )| A、25π | B、16π | C、15π | D、13π |
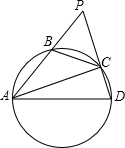 如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=
如图,已知ABCD是一个半径为R的圆内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,∠APD=60°,则R=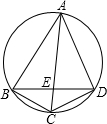 如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于
如图,已知ABCD是圆的内接四边形,对角线AC和BD相交于E,BC=CD=4,AE=6,如果线段BE和DE的长都是整数,则BD的长等于 如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.