题目内容
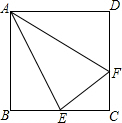 如图,已知E是正方形ABCD的边CD的中点,点F在边CD上,且∠BAE=∠FAE,
如图,已知E是正方形ABCD的边CD的中点,点F在边CD上,且∠BAE=∠FAE,求证:AF=AD+CF.
分析:过E点作EG⊥AF,垂足为G,根据题干条件首先证明△ABE≌△AGE,即可得AG=AB,同理证明出CF=GF,于是结论可以证明.
解答:证明:过E点作EG⊥AF,垂足为G,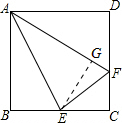
∵∠BAE=∠EAF,∠B=∠AGE=90°,
又∵∠BAE=∠EAF,即AE为角平分线,EB⊥AB,EG⊥AG,
∴BE=EG,
在Rt△ABE和Rt△AGE中,
,
∴Rt△ABE≌Rt△AGE(HL),
∴AG=AB,
同理可知CF=GF,
∴AF=BC+FC=AD+CF.

∵∠BAE=∠EAF,∠B=∠AGE=90°,
又∵∠BAE=∠EAF,即AE为角平分线,EB⊥AB,EG⊥AG,
∴BE=EG,
在Rt△ABE和Rt△AGE中,
|
∴Rt△ABE≌Rt△AGE(HL),
∴AG=AB,
同理可知CF=GF,
∴AF=BC+FC=AD+CF.
点评:本题主要考查正方形的性质和全等三角形的判定与性质的知识点,解答本题的关键是熟练掌握正方形的性质,此题难度不大.

练习册系列答案
相关题目
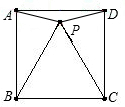 如图,已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径为a,则正方形ABCD边长为(
如图,已知P是正方形ABCD内一点,△PBC是等边三角形,若△PAD的外接圆半径为a,则正方形ABCD边长为(A、
| ||||
B、
| ||||
| C、a | ||||
D、
|
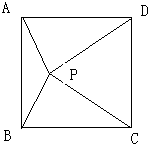 15、如图,已知P是正方形ABCD内一点,要使△APD≌△BPC,只需增加的一个条件是
15、如图,已知P是正方形ABCD内一点,要使△APD≌△BPC,只需增加的一个条件是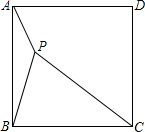 如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,PA=1,PB=2,PC=3,以点B为旋转中心,将△ABP沿顺时针方向旋转,使点A与点C重合,这时P点旋转到G点.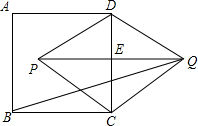 如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为
如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么tan∠PQB的值为