题目内容
【题目】写出命题“等腰三角形底边上的角平分线与中线互相重合”的逆命题,并用推理的方法证明你所写的这个逆命题是真命题.
逆命题:___________________;
已知:____________________;
求证:___________________.
证明:
【答案】如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形.
【解析】
根据逆命题的概念写出逆命题;写出已知,求证,证明△ADB≌△ADC,根据全等三角形的性质证明结论.
定理“等腰三角形底边上的角平分线与中线互相重合”的逆命题为:如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形;
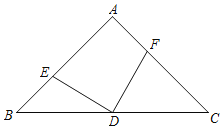
已知:如图,△ABC中,AD⊥BC,BD=DC,

求证:△ABC是等腰三角形
证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ADB和△ADC中,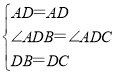 ,
,
∴△ADB≌△ADC(SAS).
∴AB=AC,即△ABC是等腰三角形;
故答案为:如果一个三角形一边上的高线和中线互相重合,那么这个三角形是等腰三角形.

练习册系列答案
相关题目