Question

【题目】直线与两坐标轴交于、两点，以为斜边在第二象限内作等腰，的图象过点，则________．

Answer 1

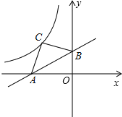
【答案】-9

【解析】

过C点作CD⊥x轴于D，CE⊥y轴于E，先确定A点坐标为（4，0），B点坐标为（0，2），再利用勾股定理计算出AB＝2，然后根据等腰三角形的性质得到∠ACB＝90°，CA＝CB＝AB＝，由于∠DCE＝90°，根据等角的余角相等得到∠ACD＝∠BCE，易证得Rt△ACD≌Rt△BCE，则CD＝CE，得到四边形CDOE为正方形，并且正方形CDOE的面积＝四边形CAOB的面积，再计算出四边形CAOB的面积＝S△CAB＋S△OAB＝CACB＋OAOB＝9，则CD＝CE＝3，可确定C点坐标为（3，3），然后把C点坐标代入反比例函数解析式即可得到k的值．

如图，过C点作CD⊥x轴于D，CE⊥y轴于E，

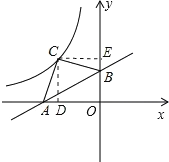
令x＝0，y＝2；令y＝0，

x＋2＝0，解得x＝4，则A点坐标为（4，0），B点坐标为（0，2），

在Rt△OAB中，OA＝4，OB＝2，

，

∵△ACB为等腰直角三角形，

∴∠ACB＝90°，CA＝CB＝AB＝，

而∠DCE＝90°，

∴∠ACD＝∠BCE，

∴Rt△ACD≌Rt△BCE，

∴CD＝CE，

∴四边形CDOE为正方形，

∴正方形CDOE的面积＝四边形CAOB的面积＝S△CAB＋S△OAB＝CACB＋OAOB＝ ×＋×4×2＝9，

∴CD＝CE＝3，

∴C点坐标为（3，3），

把C（3，3）代入y＝得k＝3×3＝9．

故答案为：9．