Question

如图，已知BE⊥AD，CF⊥AD，且BE＝CF．
（1）请你判断AD是△ABC的中线还是角平分线？并证明你的结论．
（2）在（1）的条件下，若AB＝6，AC＝4，请确定AD的值范围．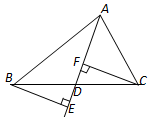

Answer 1

解：（1）AD是△ABC的中线.
理由如下：∵BE⊥AD，CF⊥AD，∴∠BED＝∠CFD＝90°
又∵BE＝CF，∠BDE＝∠CFD　∴△BDE≌△CFD（AAS）
∴BD＝CD，即AD是△ABC的中线.
（2）过点B作BG∥AC交AD延长线于点G，
∴∠GBD＝∠ACD，.
又∵AD是中线，∠BDG＝∠ADC，
∴△BDG≌△CDA（ASA），
∴BG＝AC＝4，AD＝GD，
在△ABG中，AB＝6，根据三角形三边关系，
∴2＜AG＜10，
∴1＜AD＜5.

解析