题目内容
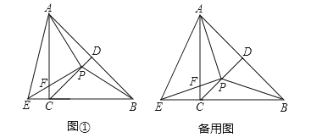
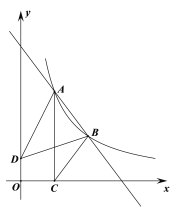
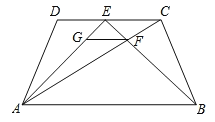
【题目】如图,在梯形ABCD中,![]() ,AD=BC,E是CD的中点,BE交AC于F,过点F作
,AD=BC,E是CD的中点,BE交AC于F,过点F作![]() ,交AE于点G.
,交AE于点G.
(1)求证:AG=BF;
(2)当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据等腰梯形的性质求得∠ADE=∠BCE,进而证得△ADE≌△BCE,得出AE=BE,根据平行线分线段成比例定理即可证得结论;
(2)先根据已知条件证得△CAB∽△CBF,证得![]() ,因为BF=AG,BC=AD,所以
,因为BF=AG,BC=AD,所以![]() ,从而证得ABAD=AGAC.
,从而证得ABAD=AGAC.
证明:(1)∵在梯形ABCD中,AB∥CD,AD=BC,
∴∠ADE=∠BCE,
在△ADE和△BCE中
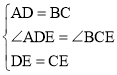
∴△ADE≌△BCE.
∴AE=BE,
∵FG∥AB,
∴![]() ,
,
∴AG=BF.
(2)∵AD2=CACF,
∴![]() ,
,
∵AD=BC,
∴![]() .
.
∵∠BCF=∠ACB,
∴△CAB∽△CBF.
∴![]() .
.
∵BF=AG,BC=AD,
∴![]() .
.
∴ABAD=AGAC.

练习册系列答案
相关题目
【题目】若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则下列说法错误的是( )
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … |
|
|
|
|
| … |
A. 二次函数图像与x轴交点有两个
B. x≥2时y随x的增大而增大
C. 二次函数图像与x轴交点横坐标一个在-1~0之间,另一个在2~3之间
D. 对称轴为直线x=1.5