题目内容
用半径为3cm，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为 cm．
考点：圆锥的计算
专题：
分析：利用圆锥的侧面展开图中扇形的弧长等于圆锥底面的周长可得．
解答：解：设此圆锥的底面半径为r，由题意，得
2πr=
，
解得r=1cm．
故答案为：1．
2πr=
| 120π×3 |
| 180 |
解得r=1cm．
故答案为：1．
点评：本题考查了圆锥的计算，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．本题就是把扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
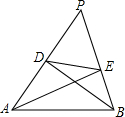已知：在△PAB中，AE⊥BP，BD⊥AP，求证：△PDE∽△PBA．
如图，D、E、F为△ABC的三边中点，L、M、N分别是△DEF三边的中点，若△ABC的周长为20cm，则△LMN的周长是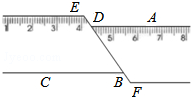
如图，一把矩形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE=128°，则∠DBC的度数为
（1）如图中的大长方形，其面积用四个小长方形面积表示为：
如图所示，某公园入口处原有三级台阶，每级台阶高20cm，宽为30cm，为方便残疾人士，拟将台阶改为斜坡，现台阶的起点为A，斜坡的起始点为C，现将坡角∠BCA设计为30°，则AC的长度应为
如图，在△ABC中，E为边AB的中点，D为边BC的中点，连接ED并延长到F，使DF=ED，求证：四边形AEFC为平行四边形．