题目内容
（2012•瑶海区三模）下列二次函数解析式中，其图象与y轴的交点在x轴下方的是（ ）
分析：令x=0，分别计算四个函数所对应的函数值，即得到它们与y轴的交点坐标，然后进行判断．
解答：解：A、令x=0，得y=3，则抛物线y=x2+3与y轴的交点坐标为（0，3），所以A选项错误；
B、令x=0，得y=-3，则抛物线y=x2-3与y轴的交点坐标为（0，-3），所以B选项正确；
C、令x=0，得y=3，则抛物线y=-x2+3与y轴的交点坐标为（0，3），所以C选项错误；
D、令x=0，得y=0，则抛物线y=x2与y轴的交点坐标为（0，0），所以D选项错误．
故选B．
B、令x=0，得y=-3，则抛物线y=x2-3与y轴的交点坐标为（0，-3），所以B选项正确；
C、令x=0，得y=3，则抛物线y=-x2+3与y轴的交点坐标为（0，3），所以C选项错误；
D、令x=0，得y=0，则抛物线y=x2与y轴的交点坐标为（0，0），所以D选项错误．
故选B．
点评：本题考查了二次函数图象上点的坐标特征：二次函数y=ax2+bx+c（a≠0）的图象上的点的坐标满足其解析式．
练习册系列答案
阅读快车系列答案
相关题目
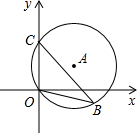（2012•瑶海区三模）如图，直径为10的⊙A经过点C和点O，点B是y轴右侧⊙A优弧上一点，∠OBC=30°，则点C的坐标为（ ）
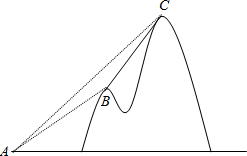（2012•瑶海区三模）如图，某电信公司计划修建一条连接B、C两地的电缆．测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B处测得C地的仰角为60°，已知C地比A地高200m，求电缆BC的长．（结果可保留根号）
（2012•瑶海区三模）姚明将带队来我市体育馆进行表演比赛，市体育局在策划本次活动，在与单位协商团购票时推出两种方案．设购买门票数为x（张），总费用为y（元）．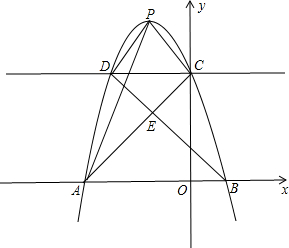
（2012•瑶海区三模）已知抛物线y=ax2+bx+c（a≠0）过点A（-3，0），B（1，0），C（0，3）三点．