题目内容
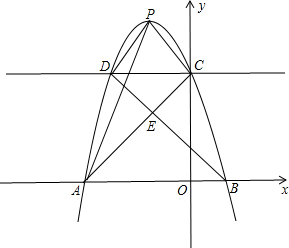 (2012•瑶海区三模)已知抛物线y=ax2+bx+c(a≠0)过点A(-3,0),B(1,0),C(0,3)三点.
(2012•瑶海区三模)已知抛物线y=ax2+bx+c(a≠0)过点A(-3,0),B(1,0),C(0,3)三点.(1)求该抛物线的函数关系式;
(2)若抛物线的顶点为P,连接PA、AC、CP,求△PAC的面积;
(3)过点C作y轴的垂线,交抛物线于点D,连接PD、BD,BD交AC于点E,判断四边形PCED的形状,并说明理由.
分析:(1)根据待定系数法将A(-3,0),B(1,0),C(0,3)三点代入解析式求出即可;
(2)利用两点之间距离公式求出PA=2
,PC=
,AC=3
,进而得出△PAC为直角三角形,求出面积即可;
(3)首先求出点D的坐标为(-2,3),PC=DP,进而得出四边形PCED是菱形,再利用∠PCA=90°,得出答案即可.
(2)利用两点之间距离公式求出PA=2
| 5 |
| 2 |
| 2 |
(3)首先求出点D的坐标为(-2,3),PC=DP,进而得出四边形PCED是菱形,再利用∠PCA=90°,得出答案即可.
解答:(1)由题意得:
,
解得:
,
∴y=-x2-2x+3;
(2)∵y=-x2-2x+3=-(x+1)2+4,
∴P(-1,4),
∵A(-3,0),B(1,0),C(0,3),
∴PA=2
,PC=
,AC=3
,
∵PA2=PC2+AC2,
∴∠PCA=90°,
∴S△APC=
×AC×PC=
×
×3
=3;
(3)四边形PCED是正方形,
∵点C与点D关于抛物线的对称轴对称,点P为抛物线的顶点,
∴点D的坐标为(-2,3),PC=DP,
∵A(-3,0),C(0,3),代入y=ax+b,
,
解得:
,
∴直线AC的函数关系式是:y=x+3,
同理可得出:直线DP的函数关系式是:y=x+5,
∴AC∥DP,
同理可得:PC∥BD,
∴四边形PCED是菱形,
又∵∠PCA=90°,
∴四边形PCED是正方形.
|
解得:
|
∴y=-x2-2x+3;
(2)∵y=-x2-2x+3=-(x+1)2+4,
∴P(-1,4),
∵A(-3,0),B(1,0),C(0,3),
∴PA=2
| 5 |
| 2 |
| 2 |

∵PA2=PC2+AC2,
∴∠PCA=90°,
∴S△APC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
(3)四边形PCED是正方形,
∵点C与点D关于抛物线的对称轴对称,点P为抛物线的顶点,
∴点D的坐标为(-2,3),PC=DP,
∵A(-3,0),C(0,3),代入y=ax+b,
|
解得:
|
∴直线AC的函数关系式是:y=x+3,
同理可得出:直线DP的函数关系式是:y=x+5,
∴AC∥DP,
同理可得:PC∥BD,
∴四边形PCED是菱形,
又∵∠PCA=90°,
∴四边形PCED是正方形.
点评:此题考查了二次函数解析式的确定、函数图象交点坐标的求法以及菱形与正方形的判定方法,难度不大,细心求解即可.

练习册系列答案
相关题目
 (2012•瑶海区三模)如图,直径为10的⊙A经过点C和点O,点B是y轴右侧⊙A优弧上一点,∠OBC=30°,则点C的坐标为( )
(2012•瑶海区三模)如图,直径为10的⊙A经过点C和点O,点B是y轴右侧⊙A优弧上一点,∠OBC=30°,则点C的坐标为( )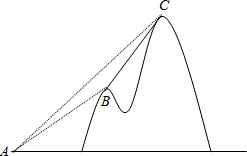 (2012•瑶海区三模)如图,某电信公司计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B处测得C地的仰角为60°,已知C地比A地高200m,求电缆BC的长.(结果可保留根号)
(2012•瑶海区三模)如图,某电信公司计划修建一条连接B、C两地的电缆.测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B处测得C地的仰角为60°,已知C地比A地高200m,求电缆BC的长.(结果可保留根号) (2012•瑶海区三模)姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).
(2012•瑶海区三模)姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).