题目内容
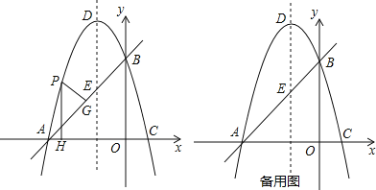
【题目】如图,在平面直角坐标系![]() 中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
中,直线y=x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线y=-x2+bx+c交x轴于另一点C,点D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)点P是直线AB上方的抛物线上一点(不与点A、B重合),过点P作x轴的垂线交x轴于点H,交直线AB于点F,作PG⊥AB于点G.求出△PFG的周长最大值;
(3)在抛物线![]() 上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
上是否存在除点D以外的点M,使得△ABM与△ABD的面积相等?若存在,请求出此时点M的坐标;若不存在,请说明理由.
【答案】(1)y=-x2-2x+3;(2)![]() .(3)M1(-2,3),M2(
.(3)M1(-2,3),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ).
).
【解析】
试题分析:(1)将已知点的坐标代入二次函数的解析式利用待定系数法确定二次函数的解析式即可;
(2)首先根据△PFG是等腰直角三角形,设P(m,-m2-2m+3)得到F(m,m+3),进而得到PF=-m2-2m+3-m-3=-m2-3m,从而得到△PFG周长为:-m2-3m+![]() (-m2-3m),配方后即可确定其最大值;
(-m2-3m),配方后即可确定其最大值;
(3)当DM1∥AB,M3M2∥AB,且与AB距离相等时,根据同底等高可以确定△ABM与△ABD的面积相等,分别求得直线DM1解析式为:y=x+5和直线M3M2解析式为:y=x+1,联立之后求得交点坐标即可.
试题解析:(1)∵直线AB:y=x+3与坐标轴交于A(-3,0)、B(0,3),
代入抛物线解析式y=-x2+bx+c中,得:
![]() ,
,
∴![]()
∴抛物线解析式为:y=-x2-2x+3;
(2)∵由题意可知△PFG是等腰直角三角形,
设P(m,-m2-2m+3),
∴F(m,m+3),
∴PF=-m2-2m+3-m-3=-m2-3m,
△PFG周长为:-m2-3m+![]() (-m2-3m),
(-m2-3m),
=-(![]() +1)(m+
+1)(m+![]() )2+
)2+![]() ,
,
∴△PFG周长的最大值为:![]() .
.
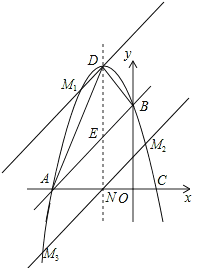
(3)点M有三个位置,如图所示的M1、M2、M3,都能使△ABM的面积等于△ABD的面积.
此时DM1∥AB,M3M2∥AB,且与AB距离相等,
∵D(-1,4),
∴E(-1,2)、则N(-1,0)
∵y=x+3中,k=1,
∴直线DM1解析式为:y=x+5,
直线M3M2解析式为:y=x+1,
∴x+5=-x2-2x+3或x+1=-x2-2x+3,
∴x1=-1,x2=-2,x3=![]() ,x4=
,x4=![]() ,
,
∴M1(-2,3),M2(![]() ,
,![]() ),M3(
),M3(![]() ,
,![]() ).
).