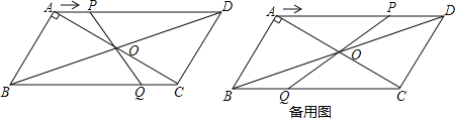
题目内容
【题目】规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如2÷2÷2，（-3）÷（-3）÷（-3）÷（-3）等．类比有理数的乘方，我们把2÷2÷2记作2③，读作“2的圈3次方”，（-3）÷（-3）÷（-3）÷（-3）记作（-3）④，读作“-3的圈4次方”，一般地，把
（a≠0）记作a，读作“a的圈n次方”．
（初步探究）
（1）直接写出计算结果：2③=___，（
）⑤=___；
（2）关于除方，下列说法错误的是___
A．任何非零数的圈2次方都等于1；
B．对于任何正整数n，1=1；
C．3④=4③；
D．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数．
（深入思考）
我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？
（1）试一试：仿照上面的算式，将下列运算结果直接写成幂的形式．
（-3）④=___；5⑥=___；（-）⑩=___．
（2）想一想：将一个非零有理数a的圈n次方写成幂的形式等于___；
（3）算一算：
÷(
)④×(2)⑤()⑥÷
【答案】初步探究：（1）
，8;（2）C；深入思考：（1）
，
，
；（2）
；（3）-5.
【解析】
初步探究：
（1）根据除方运算的定义即可得出答案；
（2）根据除方运算的定义逐一判断即可得出答案；
深入思考：
（1）根据除方运算的定义即可得出答案；
（2）根据（1）即可总结出（2）中的规律；
（3）先按照除方的定义将每个数的圈n次方算出来，再根据有理数的混合运算法则即可得出答案.
解：初步探究：
（1）2③=2÷2÷2=
（）⑤=
（2）A：任何非零数的圈2次方就是两个相同数相除，所以都等于1，故选项A错误;
B：因为多少个1相除都是1，所以对于任何正整数n，1都等于1，故选项B错误；
C：3④=3÷3÷3÷3=
，4③=4÷4÷4=
，3④≠4③，故选项C正确；
D：负数的圈奇数次方，相当于奇数个负数相除，则结果是负数；负数的圈偶数次方，相当于偶数个负数相除，则结果是正数，故选项D错误；
故答案选择：C.
深入思考：
（1）（-3）④=(-3)÷(-3)÷(-3) ÷(-3)=
5⑥=5÷5÷5÷5÷5÷5=
（-）⑩=
（2）a=a÷a÷a…÷a=
（3）原式=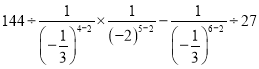
=
=
=-5
