Question

【题目】如图，在矩形ABCD中，AB＝1，BC＝3．

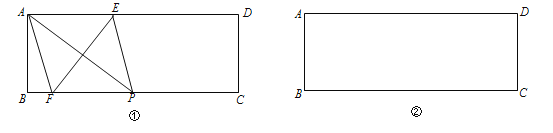
（1）在图①中，P是BC上一点，EF垂直平分AP，分别交AD、BC边于点E、F，求证：四边形AFPE是菱形；

（2）在图②中利用直尺和圆规作出面积最大的菱形，使得菱形的四个顶点都在矩形ABCD的边上，并直接标出菱形的边长．（保留作图痕迹，不写作法）

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据矩形的性质和EF垂直平分AP推出AF＝PF＝AE＝PE即可判断；

（2）以矩形的一条对角线和这条对角线的垂直平分线作菱形的对角线，此时的菱形即为矩形ABCD内面积最大的菱形．

（1）证明：如图①

∵四边形ABCD是矩形，

∴AD∥BC，

∴∠1＝∠2，

∵EF垂直平分AP，

∴AF＝PF，AE＝PE，

∴∠2＝∠3，

∴∠1＝∠3，

∴AE＝AF，

∴AF＝PF＝AE＝PE，

∴四边形AFPE是菱形；

（2）如图②，以矩形的一条对角线和这条对角线的垂直平分线作菱形的对角线，连接各个点，所得的菱形即为矩形ABCD内面积最大的菱形；

此时设菱形边长为x，

则可得12+（3-x）2=x2，

解得x=，

所以菱形的边长为．