��Ŀ����
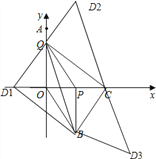
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A (0��4)������P��ԭ��O��������x����������ÿ��2����λ���ٶ��˶���ͬʱ����Q�ӵ�A��������y�Ḻ������ÿ��1����λ���ٶ��˶�����QO��QPΪ�ڱ߹���ƽ���ı���OQPB�����߶�OP���ӳ��߳�ȡ��C��ʹ��PC��2������BC��CQ�����P��Q�˶���ʱ��Ϊt(0<t<4)�룮
(1) �ú�t�Ĵ���ʽ��ʾ:
��B������___________����C������____________��
(2) ��t��1ʱ����
����ƽ���ڴ���һ��D��ʹ���Ե�Q��B��C��DΪ������ı�����ƽ���ı��Σ�ֱ��д����ʱ��D�����꣮

���𰸡���1��B��2t��t��4����C��2+2t��0������2����12���� D1����2��0����D2��2��6������D3��6����6��.
�������������������1������ƽ���ı��ε����ʵó�QO=PB�������ó���B��C�����꼴�ɣ���2������ƽ���ı��ε������г���D����������ó����꼴��.
�����������1�����P�˶���ʱ��Ϊt��
�ɵã�OP=2t��QO=OA-AQ=4-t��
���Ե�B������Ϊ��2t��t-4������C������Ϊ��2+2t��0����
��2���� 12
��Ҫʹ�Ե�Q��B��C��DΪ������ı�����ƽ���ı��Σ�
��ɵõ�D�����������������
��QD��BC����t=1ʱ��OD1=PC=2���ʵ�D1������Ϊ����2��0����
��QD��BC����t=1ʱ����B������Ϊ��2����3����3+3=6���ʿɵõ�D2������Ϊ��2��6����
��QB��DC����t=1ʱ����C������Ϊ��4��0�����ʿɵõ�D3������Ϊ��6����6��.

 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�