题目内容
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与
两点,与![]() 轴正半轴交于点
轴正半轴交于点![]() .
.
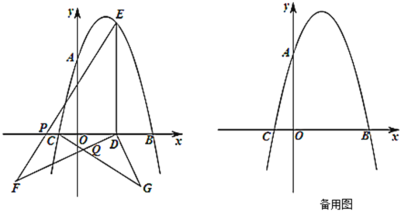
(1)求抛物线的解析式;
(2)![]() 为线段
为线段![]() 上一点,过
上一点,过![]() 作
作![]() 轴的垂线,交抛物线于点
轴的垂线,交抛物线于点![]() ,将线段
,将线段![]() ,
,![]() 绕点
绕点![]() 逆时针旋转任意相同的角到
逆时针旋转任意相同的角到![]() ,
,![]() 的位置,使点
的位置,使点![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() 都在
都在![]() 轴下方,
轴下方,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() .当
.当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)![]() 在抛物线上,
在抛物线上,![]() 在坐标平面内,当以
在坐标平面内,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为矩形时,直接写出点
为顶点的四边形为矩形时,直接写出点![]() 的坐标.
的坐标.
【答案】(1)抛物线的解析式是y=-x2+3x+4;(2)D点坐标为为(2,0),(3)点N的坐标(6,2)或(-6,-2)或![]() 或
或![]() .
.
【解析】
(1)把点![]() 和点
和点![]() 坐标代入抛物线解析式解出
坐标代入抛物线解析式解出![]() 和
和![]() 即可;
即可;
(2)旋转性质可证△EDP∽△GDQ,从而可得![]() ,继而可得ED=2DC,设D点坐标为(x,0),可得方程
,继而可得ED=2DC,设D点坐标为(x,0),可得方程![]() ,解之即可;
,解之即可;
(3)按ABM三点构成直角位置分三种情况讨论,画出图形,利用三角形相似和坐标系中两点距离列方程求解出M点坐标,再按平移规律可得N点坐标.
(1)解:∵抛物线y=-x2+bx+c经过A(0,4),C(-1,0)两点,
∴![]() ,
,
解得:![]() ,
,
∴抛物线的解析式是y=-x2+3x+4;
(2)∵∠EDF=∠CDG,
∴∠EDF-∠PDF=∠CDG-∠PDF,
∴∠EDP=∠GDQ,
又DE=DF,DC=DG,
∴![]() ,
,
∴△EDP∽△GDQ,
∴![]() ,
,
∴ED=2DC,
设D点坐标为(x,0)
∴![]() 解得x1=-1,x2=2
解得x1=-1,x2=2
∴D点坐标为为(2,0)
(3)点N的坐标是(6,2)或(-6,-2)或![]() 或
或![]() .
.
∵B点是抛物线y=-x2+3x+4的交点,
∴B点坐标为(4,0),
∴OB=4,
I.当![]() 时,如解图(1),过M点作MH⊥y轴,易证
时,如解图(1),过M点作MH⊥y轴,易证![]() ,
,
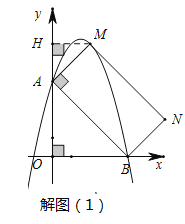
∴![]() ,
,
∴AH=HM,
设HM=x,则M点坐标为![]() ,
,
又∵点M在抛物线y=-x2+3x+4,
∴![]() ,
,
解得![]() 或
或![]() ,
,
∴M点坐标为![]() ,
,
∵四边形ABNM是矩形,根据点平移规律可知N点坐标为![]() ,
,
II.当![]() 时,如解图(2),同理可求N点坐标为
时,如解图(2),同理可求N点坐标为![]() ,
,
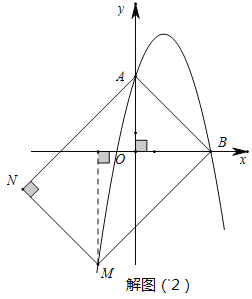
III.当![]() 时,以AB为直径作圆,交抛物线与M、
时,以AB为直径作圆,交抛物线与M、![]() ,如解图(3),
,如解图(3),
设M点坐标为(x,y),
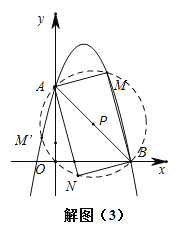
∵圆心点P坐标为(2,2),
∴MP![]()
即:![]() ,
,
又∵点M在抛物线y=-x2+3x+4,
∴
解得: ,
,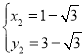 ,
,
即M点为![]() ,
,![]() ,
,
∵由点的平移规律可知,N点坐标为:![]() 或
或![]() .
.
综上所述:点N的坐标(6,2)或(-6,-2)或![]() 或
或![]() .
.

【题目】为了了解某区九年级数学教学质量检测情况,进行了抽样调查,其过程如下,请补全表一、表二中的空白,并回答提出的问题.
收集数据:随机抽取甲、乙两所学校中各自取20名学生的数学成绩进行分析
甲:91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙:84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理数据:表一
分段 学校 | 30≤x≤39 | 40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 | 0 | 0 | 1 | 2 | 8 | 5 |
分析数据:表二
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 | 88 | 91 | 268.43 |
乙 | 81.95 | 86 | 115.25 |
得出结论:
(1)若甲学校有400名九年级学生,估计这次考试成绩80分(包含80分)以上人数为 .
(2)可以推断出 (填:甲或乙)学校学生的数学水平较高,理由是 (至少从两个不同角度说明推断的合理性).
【题目】我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
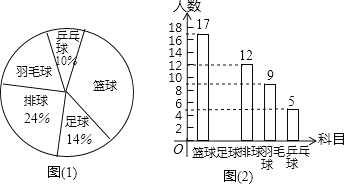
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
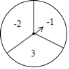
对应扇形 图中区域 | D | E | C |

(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?