题目内容
在直角坐标系中,若一点的纵横坐标都是整数,则称该点为整点.设k为整数,当直线y=x-2与y=kx+k的交点为整点时,k的值可以取
- A.4个
- B.5个
- C.6个
- D.7个
A
分析:让这两条直线的解析式组成方程组,求得整数解即可.
解答:①当k=0时,y=kx+k=0,即为x轴,则直线y=x-2和x轴的交点为(2.0)满足题意,
∴k=0
②当k≠0时,
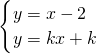 ,
,
∴x-2=kx+k,
∴(k-1)x=-(k+2),
∵k,x都是整数,k≠1,k≠0,
∴x=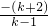 =-1-
=-1-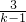 是整数,
是整数,
∴k-1=±1或±3,
∴k=2或k=4或k=-2;
综上,k=0或k=2或k=4或k=-2.
故k共有四种取值.
故选A.
点评:本题考查了一次函数与二元一次方程组,属于基础题,解决本题的难点是根据分数的形式得到相应的整数解.
分析:让这两条直线的解析式组成方程组,求得整数解即可.
解答:①当k=0时,y=kx+k=0,即为x轴,则直线y=x-2和x轴的交点为(2.0)满足题意,
∴k=0
②当k≠0时,
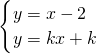 ,
,∴x-2=kx+k,
∴(k-1)x=-(k+2),
∵k,x都是整数,k≠1,k≠0,
∴x=
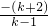 =-1-
=-1-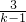 是整数,
是整数,∴k-1=±1或±3,
∴k=2或k=4或k=-2;
综上,k=0或k=2或k=4或k=-2.
故k共有四种取值.
故选A.
点评:本题考查了一次函数与二元一次方程组,属于基础题,解决本题的难点是根据分数的形式得到相应的整数解.

练习册系列答案
相关题目
 和
和 于A,B两点,P是x轴上的任意一点,则△ABP的面积等于 ▲ .
于A,B两点,P是x轴上的任意一点,则△ABP的面积等于 ▲ .