Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨Ň◊őÔŌŖ![]() £ļ
£ļ![]() ”Ž
”Ž![]() £ļ
£ļ![]() ŌŗĹĽ”ŕĶ„O°ĘC£¨
ŌŗĹĽ”ŕĶ„O°ĘC£¨![]() ”Ž
”Ž![]() ∑÷ĪūĹĽx÷Š”ŕĶ„B°ĘA£¨«“Bő™ŌŖ∂őAOĶń÷–Ķ„£ģ
∑÷ĪūĹĽx÷Š”ŕĶ„B°ĘA£¨«“Bő™ŌŖ∂őAOĶń÷–Ķ„£ģ
£®1£©«ů![]() Ķń÷Ķ£Ľ
Ķń÷Ķ£Ľ
£®2£©»ŰOC°ÕAC£¨«ů°ųOACĶń√śĽż£Ľ
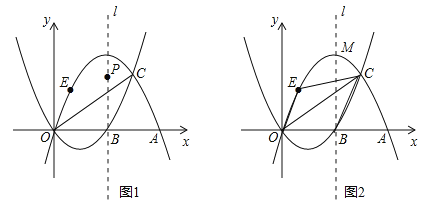
£®3£©Ň◊őÔŌŖC2Ķń∂‘≥∆÷Šő™l£¨∂•Ķ„ő™M£¨‘ŕ£®2£©ĶńŐűľĢŌ¬£ļ
ĘŔĶ„Pő™Ň◊őÔŌŖC2∂‘≥∆÷Šl…Ō“Ľ∂ĮĶ„£¨ĶĪ°ųPACĶń÷‹≥§◊Ó–° Ī£¨«ůĶ„PĶń◊ÝĪÍ£Ľ
Ęŕ»ÁÕľ2£¨Ķ„E‘ŕŇ◊őÔŌŖC2…ŌĶ„O”ŽĶ„M÷ģľš‘ň∂Į£¨ňńĪŖ–őOBCEĶń√śĽż «∑Ůīś‘ŕ◊Óīů÷Ķ£Ņ»Űīś‘ŕ£¨«ů≥Ų√śĽżĶń◊Óīů÷ĶļÕĶ„EĶń◊ÝĪÍ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ£®1£©![]() £Ľ£®2£©
£Ľ£®2£©![]() £Ľ£®3£©ĘŔP£®
£Ľ£®3£©ĘŔP£®![]() £¨
£¨![]() £©£ĽĘŕE£®
£©£ĽĘŕE£®![]() £¨
£¨![]() £©£¨
£©£¨![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
‘Ő‚∑÷őŲ£ļ£®1£©”…ŃĹŇ◊őÔŌŖĹ‚őŲ ĹŅ…∑÷Īū”√aļÕbĪŪ ĺ≥ŲA°ĘBŃĹĶ„Ķń◊ÝĪÍ£¨ņŻ”√Bő™OAĶń÷–Ķ„Ņ…Ķ√ĶĹaļÕb÷ģľšĶńĻōŌĶ Ĺ£Ľ
£®2£©”…Ň◊őÔŌŖĹ‚őŲ ĹŅ…Ō»«ůĶ√CĶ„◊ÝĪÍ£¨ĻżC◊ųCD°Õx÷Š”ŕĶ„D£¨Ņ…÷§Ķ√°ųOCD°◊°ųCAD£¨”…Ōŗň∆»żĹ«–őĶń–‘÷ Ņ…Ķ√ĶĹĻō”ŕaĶń∑Ĺ≥Ő£¨Ņ…«ůĶ√OAļÕCDĶń≥§£¨Ņ…«ůĶ√°ųOACĶń√śĽż£Ľ
£®3£©ĘŔѨŔOC”ŽlĶńĹĽĶ„ľīő™¬ķ◊„ŐűľĢĶńĶ„P£¨Ņ…«ůĶ√OCĶńĹ‚őŲ Ĺ£¨‘ÚŅ…«ůĶ√PĶ„◊ÝĪÍ£Ľ
Ęŕ…Ť≥ŲEĶ„◊ÝĪÍ£¨‘ÚŅ…ĪŪ ĺ≥Ų°ųEOBĶń√śĽż£¨ĻżĶ„E◊ųx÷ŠĶń∆Ĺ––ŌŖĹĽ÷ĪŌŖBC”ŕĶ„N£¨Ņ…Ō»«ůĶ√BCĶńĹ‚őŲ Ĺ£¨‘ÚŅ…ĪŪ ĺ≥ŲENĶń≥§£¨ĹÝ“Ľ≤ĹŅ…ĪŪ ĺ≥Ų°ųEBCĶń√śĽż£¨‘ÚŅ…ĪŪ ĺ≥ŲňńĪŖ–őOBCEĶń√śĽż£¨ņŻ”√∂ĢīőļĮ żĶń–‘÷ Ņ…«ůĶ√∆š◊Óīů÷Ķ£¨ľįEĶ„Ķń◊ÝĪÍ£ģ
‘Ő‚Ĺ‚őŲ£ļ
£®1£©‘ŕy=x2+ax÷–£¨ĶĪy=0 Ī£¨x2+ax=0£¨x1=0£¨x2=©Āa£¨°ŗB£®©Āa£¨0£©£¨‘ŕy=©Āx2+bx÷–£¨ĶĪy=0 Ī£¨©Āx2+bx=0£¨x1=0£¨x2=b£¨°ŗA£®0£¨b£©£¨°ŖBő™OAĶń÷–Ķ„£¨°ŗb=©Ā2a£¨°ŗ![]() £Ľ
£Ľ
£®2£©Ń™ŃĘŃĹŇ◊őÔŌŖĹ‚őŲ ĹŅ…Ķ√£ļ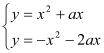 £¨ŌŻ»•y’ŻņŪŅ…Ķ√
£¨ŌŻ»•y’ŻņŪŅ…Ķ√![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() £¨
£¨![]() £¨ĶĪ
£¨ĶĪ![]() Ī£¨
Ī£¨![]() £¨°ŗC£®
£¨°ŗC£®![]() £¨
£¨![]() £©£¨ĻżC◊ųCD°Õx÷Š”ŕĶ„D£¨»ÁÕľ1£¨°ŗD£®
£©£¨ĻżC◊ųCD°Õx÷Š”ŕĶ„D£¨»ÁÕľ1£¨°ŗD£®![]() £¨0£©£¨°Ŗ°ŌOCA=90°„£¨°ŗ°ųOCD°◊°ųCAD£¨°ŗ
£¨0£©£¨°Ŗ°ŌOCA=90°„£¨°ŗ°ųOCD°◊°ųCAD£¨°ŗ![]() £¨°ŗCD2=ADOD£¨ľī
£¨°ŗCD2=ADOD£¨ľī![]() £¨°ŗa1=0£®…Š»•£©£¨
£¨°ŗa1=0£®…Š»•£©£¨![]() £®…Š»•£©£¨
£®…Š»•£©£¨![]() £¨°ŗOA=-2a=
£¨°ŗOA=-2a=![]() £¨CD=
£¨CD=![]() =1£¨°ŗ
=1£¨°ŗ![]() £Ľ
£Ľ
£®3£©ĘŔŇ◊őÔŌŖ![]() £¨°ŗ∆š∂‘≥∆÷Š
£¨°ŗ∆š∂‘≥∆÷Š![]() £¨Ķ„AĻō”ŕl2Ķń∂‘≥∆Ķ„ő™O£®0£¨0£©£¨C£®
£¨Ķ„AĻō”ŕl2Ķń∂‘≥∆Ķ„ő™O£®0£¨0£©£¨C£®![]() £¨1£©£¨‘ÚPő™÷ĪŌŖOC”Žl2ĶńĹĽĶ„£¨…ŤOCĶńĹ‚őŲ Ĺő™y=kx£¨°ŗ1=
£¨1£©£¨‘ÚPő™÷ĪŌŖOC”Žl2ĶńĹĽĶ„£¨…ŤOCĶńĹ‚őŲ Ĺő™y=kx£¨°ŗ1=![]() k£¨Ķ√k=
k£¨Ķ√k=![]() £¨°ŗOCĶńĹ‚őŲ Ĺő™
£¨°ŗOCĶńĹ‚őŲ Ĺő™![]() £¨ĶĪ
£¨ĶĪ![]() Ī£¨
Ī£¨![]() £¨°ŗP£®
£¨°ŗP£®![]() £¨
£¨![]() £©£Ľ
£©£Ľ
Ęŕ…ŤE£®m£¨![]() £©£®
£©£®![]() £©£¨‘Ú
£©£¨‘Ú![]() £¨∂ÝB£®
£¨∂ÝB£®![]() £¨0£©£¨C£®
£¨0£©£¨C£®![]() £¨1£©£¨…Ť÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y=kx+b£¨”…
£¨1£©£¨…Ť÷ĪŌŖBCĶńĹ‚őŲ Ĺő™y=kx+b£¨”…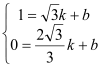 £¨Ĺ‚Ķ√£ļk=
£¨Ĺ‚Ķ√£ļk=![]() £¨b=-2£¨°ŗ÷ĪŌŖBCĶńĹ‚őŲ Ĺő™
£¨b=-2£¨°ŗ÷ĪŌŖBCĶńĹ‚őŲ Ĺő™![]() £¨ĻżĶ„E◊ųx÷ŠĶń∆Ĺ––ŌŖĹĽ÷ĪŌŖBC”ŕĶ„N£¨»ÁÕľ2£¨‘Ú
£¨ĻżĶ„E◊ųx÷ŠĶń∆Ĺ––ŌŖĹĽ÷ĪŌŖBC”ŕĶ„N£¨»ÁÕľ2£¨‘Ú![]() £¨ľīx=
£¨ľīx=![]()
°ŗEN=![]()
°ŗ![]()
°ŗSňńĪŖ–őOBCE=S°ųOBE+S°ųEBC![]()
![]() £¨°Ŗ
£¨°Ŗ![]() £¨°ŗĶĪ
£¨°ŗĶĪ![]() Ī£¨
Ī£¨![]() £¨ĶĪ
£¨ĶĪ![]() Ī£¨
Ī£¨![]() £¨°ŗE£®
£¨°ŗE£®![]() £¨
£¨![]() £©£¨
£©£¨![]() £ģ
£ģ


 ĹūŇ∆ĹŐł®Ňŗ”Ҕҗ°ĺŪ∆ŕń©≥ŚīŐ100∑÷ŌĶŃ–īūįł
ĹūŇ∆ĹŐł®Ňŗ”Ҕҗ°ĺŪ∆ŕń©≥ŚīŐ100∑÷ŌĶŃ–īūįł