题目内容
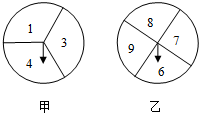 如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字.同时转动两个转盘,当转盘停止后,计算指针所指区域内的数字之和.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
如图是两个可以自由转动的转盘,甲转盘被等分成3个扇形,乙转盘被等分成4个扇形,每一个扇形上都标有相应的数字.同时转动两个转盘,当转盘停止后,计算指针所指区域内的数字之和.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.(1)请你通过画树状图或列表的方法分析,并求指针所指区域内的数字和小于10的概率;
(2)小亮和小颖小亮和小颖利用它们做游戏,游戏规则是:指针所指区域内的数字和小于10,小颖获胜;指针所指区域内的数字之和等于10,为平局;指针所指区域内的数字之和大于10,小亮获胜.你认为该游戏规则是否公平?请说明理由;若游戏规则不公平,请你设计出一种公平的游戏规则.
分析:(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后根据概率公式求出该事件的概率.
(2)判断游戏的公平性,首先要计算出游戏双方赢的概率,概率相等则公平,否则不公平.
(2)判断游戏的公平性,首先要计算出游戏双方赢的概率,概率相等则公平,否则不公平.
解答:解:(1)共有12种等可能的结果,小于10的情况有4种,
所以指针所指区域内的数字和小于10的概率为
.
(2)不公平,因为小颖获胜的概率为
=
;
小亮获胜的概率为
.小亮获胜的可能性大,
所以不公平.
可以修改为若这两个数的和为奇数,则小亮赢;积为偶数,则小颖赢.
所以指针所指区域内的数字和小于10的概率为
| 1 |
| 3 |
| 和 | 1 | 3 | 4 |
| 6 | 7 | 9 | 10 |
| 7 | 8 | 10 | 11 |
| 8 | 9 | 11 | 12 |
| 9 | 10 | 12 | 13 |
| 3 |
| 12 |
| 1 |
| 4 |
小亮获胜的概率为
| 5 |
| 12 |
所以不公平.
可以修改为若这两个数的和为奇数,则小亮赢;积为偶数,则小颖赢.
点评:本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.
于10,小亮获胜.如果指针恰好指在分割线上,那么重转一次,直到指针指向一个数字为止.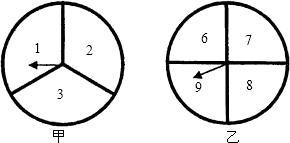
 如图是两个可以自由转动的转盘,转盘各被等分成三个扇形,并分别标上1,2,3和6,7,8这6个数字.如果同时转动两个转盘各一次(指针落在等分线上重转),转盘停止后,则指针指向的数字和为偶数的概率是( )
如图是两个可以自由转动的转盘,转盘各被等分成三个扇形,并分别标上1,2,3和6,7,8这6个数字.如果同时转动两个转盘各一次(指针落在等分线上重转),转盘停止后,则指针指向的数字和为偶数的概率是( ) 小强获胜.如果指针恰好指在分割线上,那么重转一次.
小强获胜.如果指针恰好指在分割线上,那么重转一次.