题目内容
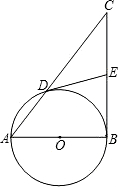 已知:如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.
已知:如图,以△ABC的边AB为直径的⊙O交边AC于点D,且过点D的切线DE平分边BC.(1)BC与⊙O是否相切?请说明理由;
(2)当△ABC满足什么条件时,以点O,B,E,D为顶点的四边形是平行四边形?并说明理由.
分析:(1)连接OD,BD,根据已知及圆周角定理等可求得∠ABC=90°,OD是半径,故BC与⊙O相切.
(2)若四边形OBED是平行四边形,应有OD∥BC,OD=BE;而BE=CE,所以BC=2BE=2OD=AB,故此时△ABC是等腰直角三角形.
(2)若四边形OBED是平行四边形,应有OD∥BC,OD=BE;而BE=CE,所以BC=2BE=2OD=AB,故此时△ABC是等腰直角三角形.
解答: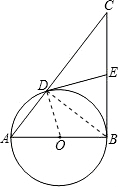 解:(1)BC与⊙O相切;
解:(1)BC与⊙O相切;
理由:连接OD,BD;
∵DE切⊙O于D,AB为直径,
∴∠EDO=∠ADB=90°,
∵DE平分CB,
∴DE=
BC=BE,
∴∠EDB=∠EBD;
∵∠ODB=∠OBD,∠ODB+∠EDB=90°,
∴∠OBD+∠DBE=90°,
即∠ABC=90°,
∴BC与⊙O相切;
(2)当△ABC为等腰直角三角形(∠ABC=90°)时,四边形OBED是平行四边形;
∵△ABC是等腰直角三角形(∠ABC=90°),
∴AB=BC,
∵BD⊥AC于D,
∴D为AC中点,
∴OD=
BC=BE,OD∥BC,
∴四边形OBED是平行四边形.
 解:(1)BC与⊙O相切;
解:(1)BC与⊙O相切;理由:连接OD,BD;
∵DE切⊙O于D,AB为直径,
∴∠EDO=∠ADB=90°,
∵DE平分CB,
∴DE=
| 1 |
| 2 |
∴∠EDB=∠EBD;
∵∠ODB=∠OBD,∠ODB+∠EDB=90°,
∴∠OBD+∠DBE=90°,
即∠ABC=90°,
∴BC与⊙O相切;
(2)当△ABC为等腰直角三角形(∠ABC=90°)时,四边形OBED是平行四边形;
∵△ABC是等腰直角三角形(∠ABC=90°),
∴AB=BC,
∵BD⊥AC于D,
∴D为AC中点,
∴OD=
| 1 |
| 2 |
∴四边形OBED是平行四边形.
点评:本题考查直角三角形的性质,圆周角定理及切线的判定等知识的综合运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
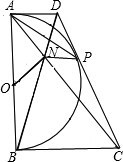 已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A,B),过点P作半圆O的切线分别交过A,B两点的切线于D,C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP•PC为定值;④PA为∠NPD的平分线.其中一定成立的是( )
已知:如图,以定线段AB为直径作半圆O,P为半圆上任意一点(异于A,B),过点P作半圆O的切线分别交过A,B两点的切线于D,C,AC、BD相交于N点,连接ON、NP.下列结论:①四边形ANPD是梯形;②ON=NP;③DP•PC为定值;④PA为∠NPD的平分线.其中一定成立的是( )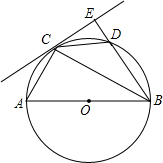 已知:如图,以Rt△ABC的斜边AB为直径作⊙O,D是⊙O上的点,且有AC=CD.过点C作⊙O的切线,与BD的延长线交于点E,连接CD.
已知:如图,以Rt△ABC的斜边AB为直径作⊙O,D是⊙O上的点,且有AC=CD.过点C作⊙O的切线,与BD的延长线交于点E,连接CD.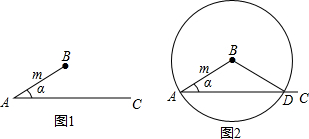

 已知:如图,以△ABC的一边BC为直径作半圆,交AB于E,过E点作半圆O的切线恰与AC垂直,试确定边BC与AC的大小关系,并证明你的结论.
已知:如图,以△ABC的一边BC为直径作半圆,交AB于E,过E点作半圆O的切线恰与AC垂直,试确定边BC与AC的大小关系,并证明你的结论.