题目内容
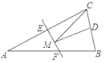
【题目】如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点。
![]()
(1)若线段AB=a,CE=b,且![]() ,求a,b的值;
,求a,b的值;
(2)在(1)的条件下,求线段CD的长.
【答案】(1)a=15,b=4.5;(2)1.5.
【解析】
(1)由![]() ,根据非负数的性质即可推出a、b的值;
,根据非负数的性质即可推出a、b的值;
(2)根据(1)所推出的结论,即可推出AB和CE的长度,根据C为线段AB的中点AC=7.5,然后由AE=AC+CE,即可推出AE的长度,由D为AE的中点,即可推出DE的长度,再根据线段的和差关系可求出CD的长度.
(1)∵![]() ,
,
∴![]() =0,
=0,![]() =0,
=0,
∵a、b均为非负数,
∴a=15,b=4.5,
(2)∵点C为线段AB的中点,AB=15,
∴![]() ,
,
∵CE=4.5,
∴AE=AC+CE=12,
∵点D为线段AE的中点,
∴DE=![]() AE=6,
AE=6,
∴CD=DECE=64.5=1.5.

【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式.(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?