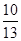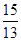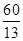题目内容
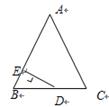
如图,△ABC中,AB=AC,D在AB上,F在AC的延长线上,且BD=CF,连接DE交BC于E.
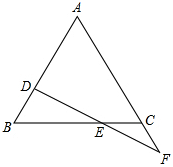
求证:DE=EF.

求证:DE=EF.
见解析
此题考查的是全等三角形的判定和性质
过D点作AF的平行线交BC于G点,利用等腰三角形的性质和平行线的性质,求证△DGE≌△FCE即可,
如图,过D点作AF的平行线交BC于G点,
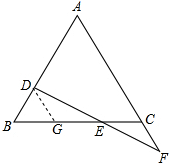
∴∠ECF=∠DGE,
∴∠DGB=∠ACB
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC=∠DGB,
∴DG=BD,
∵BD=CF,
∴DG=CF.
由∠ECF=∠DGE,∠DEG=∠CEF,DG=CF可得
△DGE≌△FCE(AAS),
∴DE=EF.
过D点作AF的平行线交BC于G点,利用等腰三角形的性质和平行线的性质,求证△DGE≌△FCE即可,
如图,过D点作AF的平行线交BC于G点,

∴∠ECF=∠DGE,
∴∠DGB=∠ACB
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC=∠DGB,
∴DG=BD,
∵BD=CF,
∴DG=CF.
由∠ECF=∠DGE,∠DEG=∠CEF,DG=CF可得
△DGE≌△FCE(AAS),
∴DE=EF.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目

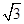 ,c=2
,c=2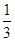 ,b=
,b=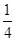 ,c=
,c=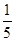
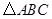 中,
中,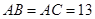 ,
,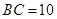 ,点
,点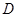 为
为 的中点,
的中点,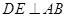 ,垂足为点
,垂足为点 ,则
,则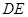 等于
等于