题目内容
【题目】如图,正方形ABCD中点E为AD的中点,连接CE,将△CDE绕点C逆时针旋转得△CGF,点G在CE上,作DM⊥CE于点M,连接BM交CF于N,已知四边形GFNM面积为27,则正方形ABCD的边长为_________.
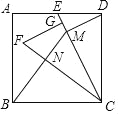
【答案】10![]()
【解析】
作BH⊥EC于H,可证△BCH≌△DMC,可得DM=CH,根据锐角三角函数可得CM=2DM,则H是CM中点,可得∠BMC=∠BCM,再证△MNC∽△FGC,根据面积比等于相似比的平方,可求正方形ABCD的边长
作BH⊥EC于H
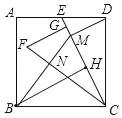
设BC=CD=AD=2a,
∵E为AD中点,
∴DE=a,
∴S△DEC=a2.
根据勾股定理得EC=![]() a,
a,
∵∠HBC+∠HCB=90°,∠ECD+∠HCB=90°,
∴∠ECD=∠HBC,且CD=BC,∠BHC=∠DMC=90°,
∴△DMC≌△BHC,
∴CH=MD,BH=CM,
∵sin∠DCE=![]() ,
,
∴![]() ,
,
∴DM=![]() a,
a,
∴CM=![]() =
=![]() a,
a,
∴CH=![]() a,
a,
∴MH=CH,且BH⊥CM,
∴BM=BC,
∴∠BMC=∠BCM,
∵AD∥BC,
∴∠DEC=∠ECB,
∵旋转
∴∠F=∠DEC,CF=CE=![]() a
a
∴∠F=∠BMC,∠MCF=∠MCF
∴△MNC∽△GFC
∴![]() ,
,
![]() ,
,
∴S△MNC=![]() ,
,
∴SFGMN=a2﹣![]() =
=![]() ,
,
∴![]() =27,
=27,
∴a=5![]() ,
,
∴2a=10![]() ,
,
故答案为:10![]()

练习册系列答案
相关题目