题目内容
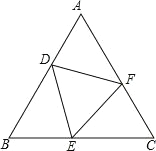
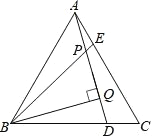
【题目】如图,在等边△ABC 中,点 D、E 分别在边 BC、AC 上,且 AE=CD,BE 与 AD 相交于点 P,BQ⊥AD 于点 Q.
(1)求证:BE=AD;
(2)若 PQ=4,求 BP 的长.
【答案】(1)见解析;(2)8.
【解析】
(1)欲证明BE=AD,只要证明△ABE≌△CAD即可;
(2)只要证明∠BPQ=60°,利用直角三角形30度角的性质即可解决问题.
证明:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=∠C=60°,
在△ABE 和△CAD 中
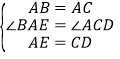 ,
,
∴△ABE≌△CAD(SAS),
∴BE=AD.
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BPQ=∠ABP+∠BAP=∠CAD+∠BAP=∠BAC=60°,
又∵BQ⊥AD,
∴∠BQP=90°,
∴∠PBQ=180°﹣∠BPQ﹣∠BQP=30°,
∴BP=2PQ,
又∵PQ=4,
∴BP=8.

【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | |
50﹣60 | 0.39 | |
60﹣70 | ||
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |

(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?