题目内容
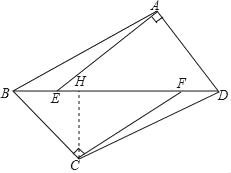
【题目】已知:如图,在四边形ABCD中,过A,C分别作AD和BC的垂线,交对角线BD于点E,F,AE=CF,BE=DF.
(1)求证:四边形ABCD是平行四边形;
(2)若BC=4,∠CBD=45°,且E,F是BD的三等分点,求四边形ABCD的面积.(直接写出结论即可)

【答案】(1)证明见解析;(2)24.
【解析】
(1)证Rt△ADE≌Rt△CBF(HL),得AD=BC,∠ADE=∠CBF,AD∥BC,故四边形ABCD是平行四边形;(2)过C作CH⊥BD于H,证△CBF是等腰直角三角形,得BF=![]() BC=4
BC=4![]() ,CH=
,CH=![]() BC=2
BC=2![]() ,得BD=6
,得BD=6![]() ,故四边形ABCD的面积=BDCH.
,故四边形ABCD的面积=BDCH.
(1)证明:∵AE⊥AD,CF⊥BC,
∴∠DAE=∠BCF=90°,
∵BE=DF,
∴BE+EF=DF+EF,
即BF=DE,
在Rt△ADE与Rt△CBF中,
![]()
∴Rt△ADE≌Rt△CBF(HL),
∴AD=BC,∠ADE=∠CBF,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)解:过C作CH⊥BD于H,
∵∠CBD=45°,
∴△CBF是等腰直角三角形,
∴BF=![]() BC=4
BC=4![]() ,CH=
,CH=![]() BC=2
BC=2![]() ,
,
∵E,F是BD的三等分点,
∴BD=6![]() ,
,
∴四边形ABCD的面积=BDCH=24.

 阅读快车系列答案
阅读快车系列答案【题目】某综合实践小组为了了解本校学生参加课外读书活动的情况,随机抽取部分学生,调查其最喜欢的图书类别,并根据调查结果绘制成如下不完整的统计表与统计图:
图书类别 | 画记 | 人数 | 百分比 | ||
文学类 | |||||
艺体类 | 正 | 5 | |||
科普类 | |||||
其他 | 正正 | 14 | |||
合计 | a | 100% |
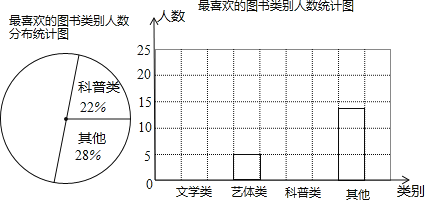
请结合图中的信息解答下列问题:
(1)随机抽取的样本容量![]() 为________;
为________;
(2)在扇形统计图中,“艺体类”所在的扇形圆心角应等于_________度;
(3)补全条形统计图;
(4)已知该校有![]() 名学生,估计全校最喜欢文学类图书的学生有________人.
名学生,估计全校最喜欢文学类图书的学生有________人.





