Question

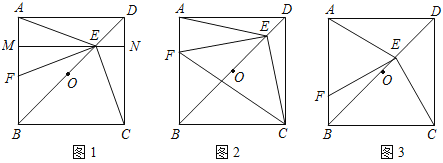
【题目】如图，四边形是正方形，是等边三角形.

(1)求证：；

(2)求的度数.

Answer 1

【答案】(1)证明见解析(2) 150°．

【解析】

试题分析：（1）根据正方形、等边三角形的性质，可以得到AB=BE=CE=CD，∠ABE=∠DCE=30°，由此即可证明；

（2）只要证明∠EAD=∠ADE=15°，即可解决问题；

试题解析：（1）证明：∵四边形ABCD是正方形，△ABC是等边三角形，

∴BA=BC=CD=BE=CE，∠ABC=∠BCD=90°，∠EBC=∠ECB=60°，

∴∠ABE=∠ECD=30°，

在△ABE和△DCE中，

，

∴△ABE≌△DCE（SAS）．

（2）∵BA=BE，∠ABE=30°，

∴∠BAE=（180°﹣30°）=75°，

∵∠BAD=90°，

∴∠EAD=90°﹣75°=15°，同理可得∠ADE=15°，

∴∠AED=180°﹣15°﹣15°=150°．