题目内容
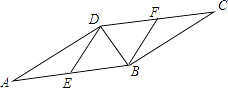
【题目】如图,在平面直角坐标系中,两个函数y=x,y=﹣![]() x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
(1)求点A的坐标.
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式.
(3)在(2)的条件下,S是否有最大值若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由.
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是 .

【答案】(1)A(4,4);(2)见解析;(3)有最大值,当t=2![]() 时,S的最大值为12;(4)t≥12
时,S的最大值为12;(4)t≥12![]() .
.
【解析】
(1)因为两个函数y=x,y=-![]() x+6的图象交于点A,所以将两个函数的解析式联立,得到方程组,解之即可;
x+6的图象交于点A,所以将两个函数的解析式联立,得到方程组,解之即可;
(2)因为点P在直线OA即y=x上以每秒1个单位的速度运动,所以OP=t,而OA是第一、三象限坐标轴夹角的平分线,所以点P坐标为(![]() t,
t,![]() t),又因PQ∥x轴交直线BC于点Q,所以可得点Q的纵坐标为
t),又因PQ∥x轴交直线BC于点Q,所以可得点Q的纵坐标为![]() t,并且点Q在y=-
t,并且点Q在y=-![]() x+6上,因此可得到关于x、t的关系式,经过变形可用t表示x,即得到点Q坐标为(12
x+6上,因此可得到关于x、t的关系式,经过变形可用t表示x,即得到点Q坐标为(12![]() t,
t,![]() t),PQ=12
t),PQ=12![]() t,当重叠部分是正方形时,分情况代入面积公式中求解;
t,当重叠部分是正方形时,分情况代入面积公式中求解;
(3)结合(2)中的关系式可知有最大值,并且最大值应在0<t≤3![]() 中,利用二次函数最值的求法就可得到S的最大值为12;
中,利用二次函数最值的求法就可得到S的最大值为12;
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积正好最大时,此时重合部分就是△AOB,B的坐标为(12,0),并且有PB⊥OB,PB=OB=12,所以OP=12![]() ,即t≥12
,即t≥12![]() .
.
(1)由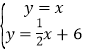 可得
可得![]() ,
,
∴A(4,4);
(2)点P在y=x上,OP=t,
则点P坐标为![]() ,
,
点Q的纵坐标为![]() ,并且点Q在y=﹣
,并且点Q在y=﹣![]() x+6上,
x+6上,
∴![]() ,
,
即点Q坐标为![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当点P到达A点时,t=2![]() ,
,
当3![]() ﹤t﹤4
﹤t﹤4![]() 时,S=
时,S=![]() ,
,
=![]() ;
;
(3)有最大值,最大值应在![]() 中,
中,
![]() ,
,
当t=2![]() 时,S的最大值为12;
时,S的最大值为12;
(4)当正方形PQMN与△OAB重叠部分面积正好最大时,此时重合部分就是△AOB,
∵B的坐标为(12,0),PB⊥OB,
∴PB=OB=12,
∴OP=12![]() ,
,
∴t≥12![]() .
.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案