题目内容

（本题满分10分），如图，在△ABC中，AD是∠BAC的平分线，M是BC的中点，过M作ME∥AD交BA延长线于E，交AC于F，求证：BE=CF=（AB+AC）。

 

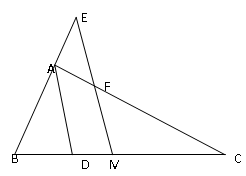
证明：延长FM至P，使MP=FM，连结BP可证△FCM△PBM

∴CF=BP，∠3=∠P

由AD∥ME，可知∠1=∠E，∠2=∠3=∠5

∴∠E=∠P   ∴BE=BP 则BE=CF

又可证∠E=∠5， ∴AE=AF

则BE+CF=AB+AE+CF=AB+AF+CF=AB+AC

∴

解析:略

 

练习册系列答案
相关题目
（本题满分10分）

如图，已知OA⊥OB，OA＝8，OB＝6，以AB为边作矩形ABCD，使AD＝a，过点D作DE垂直OA的延长线交于点E．
（1）求证：△OAB∽△EDA；                               
（2）当a为何值时，△OAB与△EDA全等？并求出此时点C到OE的距离．
（11·贵港）（本题满分10分）
随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多地进入普通家庭．据某市交通部门统计，2008年底该市汽车拥有量为75万辆，而截止到2010年底，该市的汽车拥有量已达108万辆．
（1）求2008年底至2010年底该市汽车拥有量的年平均增长率；
（2）为了保护城市环境，缓解汽车拥堵状况，该市交通部门拟控制汽车总量，要求到2012
年底全市汽车拥有量不超过125.48万辆；另据统计，从2011年初起，该市此后每年报废的
汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同，请你估算出该市从2011
年初起每年新增汽车数量最多不超过多少万辆．

（本题满分10分）如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路. 现新修一条路AC到公路l. 小明测量出∠ACD=30º，∠ABD=45º，BC=50m. 请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据：，）.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

（本题满分10分）如图，BD是直径，过⊙O上一点A作⊙O切线交DB延长线于P，过B点作BC∥PA交⊙O于C，连接AB、AC ，

1.（1）求证：AB = AC

2.（2）若PA= 10 ，PB = 5 ，求⊙O半径．

 

 

（本题满分10分）如图，已知二次函数的图象的顶点为．二次函数的图象与轴交于原点及另一点，它的顶点在函数的图象的对称轴上．

（1）求点与点的坐标；

（2）当四边形为菱形时，求函数的关系式．

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网