��Ŀ����
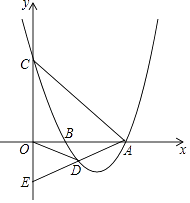
����Ŀ����ͼ��������y=mx2��16mx+48m��m��0����x�ύ��A��B���㣨��B�ڵ�A��ࣩ����y�ύ�ڵ�C����D���������ϵ�һ�����㣬��λ�ڵ������ޣ�����OD��BD��AC��AD���ӳ�AD��y���ڵ�E��
��1������OACΪ����ֱ�������Σ���m��ֵ��
��2����������m��0��C��E�����ܹ���ԭ��Գƣ����D�����꣨�ú�m��ʽ�ӱ�ʾ����
��3������D�˶���ijһλ��ʱ��ǡ��ʹ�á�ODB=��OAD���ҵ�DΪ�߶�AE���е㣬��ʱ���ڸ�������������һ��P��x0 �� y0������n+ ![]() �ݩ�4
�ݩ�4 ![]() my02��12
my02��12 ![]() y0��50��������ʵ��n����Сֵ��
y0��50��������ʵ��n����Сֵ��
���𰸡�
��1��
�⣺��y=mx2��16mx+48m=m��x��4����x��12��=0����x1=12��x2=4��
��A��12��0������OA=12��
�֡�C��0��48m����
�൱��OACΪ����ֱ��������ʱ��OA=OC��
��12=48m��
��m= ![]()
��2��
�⣺�ɣ�1����֪��C��0��48m����
�߶�����m��0��C��E�����ܹ���ԭ��Գƣ�
�����E��0����48m����
��ֱ��AE�Ľ���ʽΪy=kx+b��
��E��0����48m����A��12��0�����룬�ɵ�
![]() �����
����� ![]() ��
��
��ֱ��AE�Ľ���ʽΪy=4mx��48m��
�ߵ�DΪֱ��AE�������ߵĽ��㣬
��ⷽ���� ![]() ���ɵ�
���ɵ� ![]() ��
�� ![]() ����A��ȥ����
����A��ȥ����
����D��������8����16m��
��3��
�⣺����ODB=��OAD����DOB=��AODʱ����ODB�ס�OAD��
��OD2=OA��OB=4��12=48��
��OD=4 ![]() ��
��
�֡ߵ�DΪ�߶�AE���е㣬
��AE=2OD=8 ![]() ��
��
�֡�OA=12��
��OE= ![]() =4
=4 ![]() ��
��
��D��6����2 ![]() ����
����
��D��6����2 ![]() ������������y=mx2��16mx+48m���ɵé�2
������������y=mx2��16mx+48m���ɵé�2 ![]() =36m��96m+48m��
=36m��96m+48m��
���m= ![]() ��
��
�������ߵĽ���ʽΪy= ![]() ��x��4����x��12����
��x��4����x��12����
��y= ![]() ��x��8��2��
��x��8��2�� ![]() ��
��
�ߵ�P��x0��y0��Ϊ������������һ�㣬
��y0�ݩ� ![]() ��
��
��t=��4 ![]() my02��12
my02��12 ![]() y0��50=��2y02��12
y0��50=��2y02��12 ![]() y0��50=��2��y0+3
y0��50=��2��y0+3 ![]() ��2+4��
��2+4��
��y0�ݩ� ![]() ʱ��t���ֵ=��2����
ʱ��t���ֵ=��2���� ![]() +3
+3 ![]() ��2+4=
��2+4= ![]() ��
��
��Ҫʹn+ ![]() �ݩ�4
�ݩ�4 ![]() my02��12
my02��12 ![]() y0��50��������n+
y0��50��������n+ ![]() ��
�� ![]() ��
��
��n��3 ![]() ��
��
��ʵ��n����СֵΪ ![]() ��
��
����������1������y=mx2��16mx+48m���ɵ�A��12��0����C��0��48m�����ٸ���OA=OC�����ɵõ�12=48m�������ó�m��ֵ����2������C��E�����ܹ���ԭ��Գƣ��õ�E��0����48m��������E��0����48m����A��12��0���ɵ�ֱ��AE�Ľ���ʽ�����ⷽ���鼴�ɵõ�ֱ��AE�������ߵĽ���D�����ꣻ��3�����ݡ�ODB�ס�OAD���ɵ�OD=4 ![]() �������õ�D��6����2
�������õ�D��6����2 ![]() ��������������y=mx2��16mx+48m���ɵ������߽���ʽ���ٸ��ݵ�P��x0 �� y0��Ϊ������������һ�㣬���ɵó�y0�ݩ�
��������������y=mx2��16mx+48m���ɵ������߽���ʽ���ٸ��ݵ�P��x0 �� y0��Ϊ������������һ�㣬���ɵó�y0�ݩ� ![]() ����t=��2��y0+3
����t=��2��y0+3 ![]() ��2+4���ɵ�t���ֵ=��2����
��2+4���ɵ�t���ֵ=��2���� ![]() +3
+3 ![]() ��2+4=
��2+4= ![]() ���ٸ���n+
���ٸ���n+ ![]() ��
�� ![]() ���ɵ�ʵ��n����СֵΪ
���ɵ�ʵ��n����СֵΪ ![]() ��
��
�����㾫����ͨ��������õ���ֱ�������κ�ȷ��һ�κ����ı���ʽ�����յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ���������Խ����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ�˴����л����㴫ͳ�Ļ����н����־�����չ�������ж���У�����ijУ��ί��֯���꼶100��ѧ�����С������ж���ѡ�����������ȫ�����ѧ���ijɼ������������õ����в�������ͳ��ͼ����
��� | ������ | Ƶ�� | Ƶ�� |
A | 60��x��70 | 17 | 0.17 |
B | 70��x��80 | 30 | a |
C | 80��x��90 | b | 0.45 |
D | 90��x��100 | 8 | 0.08 |
�����������Ϣ������������⣺
��1������a= �� b=��
��2�����������ͳ��ͼ��B���Ӧ���ε�Բ�ĽǵĶ�����
��3����֪������ͬѧ��ȡ��98�ֵ���óɼ������а�������ͬһ�༶�ļס�������ͬѧ��ѧУ����������ͬѧ�����ѡ�������μ��м������������б�������״ͼ����ס�������ͬѧ����ѡ�еĸ��ʣ�




