题目内容
关于x的方程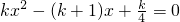 有两个实数根.(包括两个相等实数根)
有两个实数根.(包括两个相等实数根)
(1)求k的取值范围;
(2)是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
(3)若y=k(3+k)(x1+x2),k为自变量,用k表示y并求y的最大值.
解:(1)由题意可知,k≠0且△=(k+1)2-4k•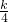 ≥0
≥0
∴k≥- 且k≠0.
且k≠0.
(2)不存在.
设方程的两根是x1,x2.x1x2= ≠0,
≠0,
∴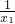 +
+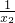 =
= =0.
=0.
∴x1+x2=0. ,
,
∴k+1=0
k=-1<- .
.
∴满足条件的实数k不存在.
(3)y=-(k+1)(k+3)=-k2-4k-3=-(k+2)2+1,
∴对称轴为k=-2,
∵k≥- 且k≠0
且k≠0
∴k=- 时有最大值y=-(-
时有最大值y=-(- +2)2+1=-
+2)2+1=- .
.
分析:(1)根据有两个实数根得到其根的判别式大于等于零,同时还应注意二次项系数;
(2)假设存在,利用两实数根的倒数和为0求得k值即可;
(3)利用求二次函数最值的方法即可求得y的最大值;
点评:本题考查了一元二次方程根与系数的关系、根的判别式及二次函数的最值的知识,知识点较多,难度适中.
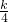 ≥0
≥0∴k≥-
 且k≠0.
且k≠0.(2)不存在.
设方程的两根是x1,x2.x1x2=
 ≠0,
≠0,∴
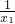 +
+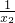 =
= =0.
=0.∴x1+x2=0.
 ,
,∴k+1=0
k=-1<-
 .
.∴满足条件的实数k不存在.
(3)y=-(k+1)(k+3)=-k2-4k-3=-(k+2)2+1,
∴对称轴为k=-2,
∵k≥-
 且k≠0
且k≠0∴k=-
 时有最大值y=-(-
时有最大值y=-(- +2)2+1=-
+2)2+1=- .
.分析:(1)根据有两个实数根得到其根的判别式大于等于零,同时还应注意二次项系数;
(2)假设存在,利用两实数根的倒数和为0求得k值即可;
(3)利用求二次函数最值的方法即可求得y的最大值;
点评:本题考查了一元二次方程根与系数的关系、根的判别式及二次函数的最值的知识,知识点较多,难度适中.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
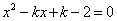 有两个正实根,求k的取值范围.
有两个正实根,求k的取值范围.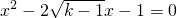 有两个不等实根,则k的取值范围是________.
有两个不等实根,则k的取值范围是________.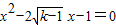 有两个不等实根,则k的取值范围是 .
有两个不等实根,则k的取值范围是 .