题目内容
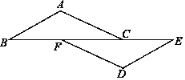
【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
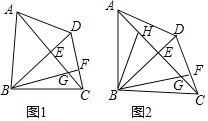
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.
【答案】(1)证明见解析;(2)△ACD、△ABE、△BCE、△BHG.
【解析】(1)由AC⊥BD、BF⊥CD知∠ADE+∠DAE=∠CGF+∠GCF,根据∠BGE=∠ADE=∠CGF得出∠DAE=∠GCF即可得;
(2)设DE=a,先得出AE=2DE=2a、EG=DE=a、AH=HE=a、CE=AE=2a,据此知S△ADC=2a2=2S△ADE,证△ADE≌△BGE得BE=AE=2a,再分别求出S△ABE、S△ACE、S△BHG,从而得出答案.
(1)∵∠BGE=∠ADE,∠BGE=∠CGF,
∴∠ADE=∠CGF,
∵AC⊥BD、BF⊥CD,
∴∠ADE+∠DAE=∠CGF+∠GCF,
∴∠DAE=∠GCF,
∴AD=CD;
(2)设DE=a,
则AE=2DE=2a,EG=DE=a,
∴S△ADE=![]() AE×DE=
AE×DE=![]() ×2a×a=a2,
×2a×a=a2,
∵BH是△ABE的中线,
∴AH=HE=a,
∵AD=CD、AC⊥BD,
∴CE=AE=2a,
则S△ADC=![]() ACDE=
ACDE=![]() (2a+2a)a=2a2=2S△ADE;
(2a+2a)a=2a2=2S△ADE;
在△ADE和△BGE中,
∵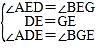 ,
,
∴△ADE≌△BGE(ASA),
∴BE=AE=2a,
∴S△ABE=![]() AEBE=
AEBE=![]() (2a)2a=2a2,
(2a)2a=2a2,
S△ACE=![]() CEBE=
CEBE=![]() (2a)2a=2a2,
(2a)2a=2a2,
S△BHG=![]() HGBE=
HGBE=![]() (a+a)2a=2a2,
(a+a)2a=2a2,
综上,面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案