Question

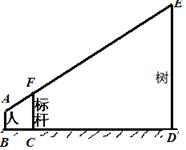
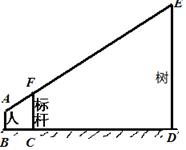
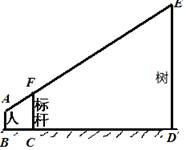
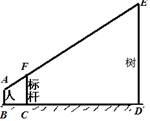
为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上，此同学眼睛距地面1.6米，标杆为3.1米，且BC=1米，CD=5米，请你根据所给出的数据求树高ED.

 

 

Answer 1

【答案】

10.6米.

【解析】

试题分析：首先做出辅助线，得出△AHF∽△AGE，进而求出GE的长，进而求出ED的长．

试题解析：如图，过点A作AG⊥DE于点G，交CF于点H．

由题意可得 四边形ABCH、ABDG、CDGH都是矩形，AB∥CF∥DE．

∴△AHF∽△AGE．∴.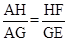

由题意可得AH=BC=1，AG=BD=6，FH=FC-HC=FC-AB=3.1-1.6=1.5．

∴．

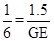∴GE=9．

∴ED=GE+DG=GE+AB=9+1.6=10.6．

答：树高ED为10.6米．

考点：相似三角形的应用．