题目内容
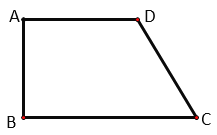
【题目】某工厂准备翻建新的大门,厂门要求设计成轴对称的拱形曲线.已知厂门的最大宽度AB=12m,最大高度OC=4m,工厂的运输卡车的高度是3m,宽度是5.8m.现设计了两种方案.方案一:建成抛物线形状(如图1);方案二:建成圆弧形状(如图2).为确保工厂的卡车在通过厂门时更安全,你认为应采用哪种设计方案?请说明理由.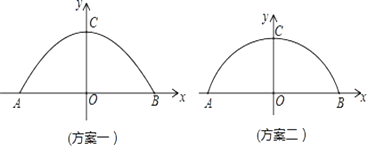
【答案】解:第一方案:设抛物线的表达式是y=a(x+6)(x6),
因C(0,4)在抛物线的图象上,代入表达式,得a= ![]() .
.
故抛物线的表达式是y= ![]() x2+4.
x2+4.
把第一象限的点(t,3)代入函数,得3= ![]() t2+4,
t2+4,
∴t=3,
∴当高度是3m时,最大宽度是6m.
第二方案:
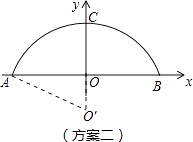
由垂径定理得:圆心O′在y轴上(原点的下方)
设圆的半径是R,在Rt△OAO′中,由勾股定理得:62+(R4)2=R2,
解得R=6.5,
当高度是3m时,最大宽度= ![]() =4
=4 ![]() ≈6.9m
≈6.9m
根据上面的计算得:为了工厂的特种卡车通过厂门更安全,所以采用第二种方案更合理.
【解析】方案一、根据已知中的AB的长,可得出此抛物线与x轴的两交点A、B的坐标,设函数解析式为交点式,再将点C的坐标代入解析式,即可求出函数解析式,然后将y=3代入求出对应的自变量的值,可得出最大宽度为6m;方案二、根据题意可知圆点在y轴的(原点)下方,连接O′A,根据垂径定理求出OA的长,然后在Rt△OAO′中,根据勾股定理建立关于R的方程,求解得出圆的半径长,再根据工厂的运输卡车的高度是3m,求出最大宽度,则宽度较大的设计方案能保工厂的卡车在通过厂门时更安全。
【考点精析】通过灵活运用勾股定理的概念和垂径定理,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧即可以解答此题.