题目内容
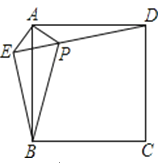
【题目】已知矩形ABCD中,AF为∠DAC的角平分线,CP⊥AF于点F,且交AD的延长线于P.连接BF交对角线AC于点O.
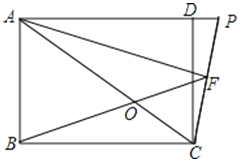
(1)若BC=4,tan∠ACB=![]() ,求
,求![]() 的值;
的值;
(2)求证:∠AOB=3∠PAF.
【答案】(1)![]() -4,(2)证明见解析
-4,(2)证明见解析
【解析】
试题分析:(1)首先根据条件证明AP=AC,然后利用tan∠ACB=![]() ,求出AB=2,然后利用勾股定理求出AC=
,求出AB=2,然后利用勾股定理求出AC=![]() ,DP=
,DP=![]() -4,再利用三角形的面积公式计算即可;(2)连接DF,根据(1)的过程得出PF=CF,进而得到∠ADF=∠BCF,然后证明△ADF≌△BCF,得出∠DAF=∠CBF,再利用角的和差关系可得出结论.
-4,再利用三角形的面积公式计算即可;(2)连接DF,根据(1)的过程得出PF=CF,进而得到∠ADF=∠BCF,然后证明△ADF≌△BCF,得出∠DAF=∠CBF,再利用角的和差关系可得出结论.
试题解析:(1)∵AF为∠DAC的角平分线,CP⊥AF,∴AP=AC,∵BC=4,tan∠ACB=![]() ,∴AB=2,根据勾股定理得AC=
,∴AB=2,根据勾股定理得AC=![]() ,∴DP=
,∴DP=![]() -4,∴S△DCP=
-4,∴S△DCP=![]()
![]() DP
DP![]() DC=
DC=![]() ×(
×(![]() -4)×2=
-4)×2=![]() -4,
-4,
(2)如图所示,连接DF,
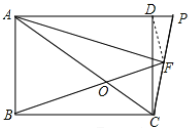
由(1)易知PF=CF,∴DF=CF,∴∠FDC=∠FCD,∴∠ADF=∠BCF,在△ADF和△BCF中,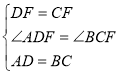 ,∴△ADF≌△BCF,∴∠DAF=∠CBF,又∵∠ACB=∠DAC=2∠DAF,∴∠AOB=∠CBF+∠ACB=3∠DAF.
,∴△ADF≌△BCF,∴∠DAF=∠CBF,又∵∠ACB=∠DAC=2∠DAF,∴∠AOB=∠CBF+∠ACB=3∠DAF.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目