��Ŀ����
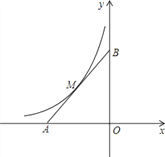
����Ŀ������������ͬһ����·��ͬʱ������ͬʱ�н����ײ��У����ﳵ������ʱ����ǰ�����ں�ͼ��l����l�����ֱ��ʾ������ס���������ص�·��s��km���;�����ʱ��t��h���Ĺ�ϵ��

��1���ҳ���ʱ�ס������___km��
��2��������һ��·�����г��������ϣ��������������õ�ʱ����___h��
��3��ͼ��l����l���ཻ��ʵ��������ʲô��
��4�����ҵ����г�û�й��ϣ����ֳ���ʱ���ٶ�ǰ������ף���������ʱ��͵ص㣮
���𰸡�(1)10;(2)1;(3) �ҳ���3Сʱʱ���ھ��ҳ�����25km�������ϼף�(4) �ھ��ҵij�����15km�������ϼ�.
����������1������ͼ��t=0ʱ������������ͼ���������IJ��������
��2�������ҵ�ͼ��ֱ����⣻
��3�����ݺ��������ʵ��Ӧ���ǹؼ���
��4�����ô���ϵ������üĺ�������ʽ�Լ��ҳ���ʱy��t�ĺ�������ʽ��Ȼ�����������ʽ��ɵķ����鼴����ã�
�⣺��1���ҳ���ʱ�ס�������10km��
��2�������������õ�ʱ����1.5-0.5=1��h����
��3����ʾ�ҳ���3Сʱʱ���ھ��ҳ�����25km�������ϼף�
��4�����ҳ���ʱ�ĺ�������ʽ��y=kt���ѣ�0.5��7.5������ã�k=15����������ʽ��y=15t��
��ĺ�������ʽ��y=mt+n��
��������ã� ![]() ,
,
��ã� ![]() ��
��
��������ʽ��y=5t+10��
��������ã�
![]() ��
��
��ã� ![]() .
.
����û�й��ϣ����ҳ���1Сʱʱ���ھ��ҵij�����15km�������ϼ�.

����Ŀ��2017��Ԫ���ڼ䣬ij�̳����������棬�����ʾ��
�Ż� ���� | һ���Թ��ﲻ����200Ԫ | һ���Թ��ﳬ��200Ԫ����������500Ԫ | һ���Թ��ﳬ��500Ԫ |
�Ż� �취 | û���Ż� | ȫ���������Ż� | ����500Ԫ�������Żݣ�����500Ԫ���ְ������Ż� |
С���������ι���ֱ�����134Ԫ��490Ԫ��
��1��С�����������ι���ʱ��������Ʒ��ԭ�۷ֱ�Ϊ���٣�
��2����С�����轫���ι������Ʒһ��ȫ�����壬�����Ǹ���ʡ���Ǹ��˷ѣ�˵˵������ɣ�