题目内容
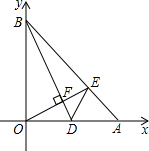
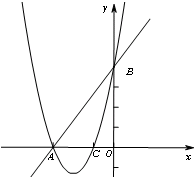
如图,直线AB交x轴于点A(2,0),交抛物线y=ax2于点B(1,| 3 |
 各顶点的距离相等,直线AC交y轴于点D.
各顶点的距离相等,直线AC交y轴于点D.(1)填空:a=
(2)连接BC与BD,求四边形OCBD的面积;
(3)当x>0时,在直线OC和抛物线y=ax2上是否分别存在点P和点Q,使四边形DOPQ为特殊的梯形?若存在,请直接写出点P的坐标;若不存在,说明理由.
分析:(1)把点B的坐标代入抛物线可以求出a的值.(2)利用两点间距离公式求出线段OA,OB以及AB的长,判断△OAB的形状.(2)结合图形求出点C,D的坐标,判断四边形OCBD是平行四边形,然后求出平行四边形的面积.
(3)从等腰梯形,直角梯形和平行四边形等几种情况直接写出点P的坐标.
(3)从等腰梯形,直角梯形和平行四边形等几种情况直接写出点P的坐标.
解答:解:(1)把点B的坐标代入抛物线有:a=
.
OA=2,OB=
=2,AB=
=2,
∴OA=OB=AB,
所以△OAB是等边三角形.
故答案是:a=
.△OAB是等边三角形;
(2)∵点C到△OAB各个顶点的距离相等,
∴点C是△OAB的外心,
∴C(1,
)
∵B(1,
),
∴BC=
.
在直角△OAD中,OA=2,∠OAD=30°,
∴OD=
.
所以四边形OCBD是平行四边形.
SOCBD=OD×1=
.
因此OCBD的面积为
;
(3)当点P(
,
),点Q(
,
)时,DOPQ是等腰梯形.
当点P(
,
),点Q(
,
)时,DOPQ是直角梯形.
∴P1(
,
),P2(
,
).
| 3 |
OA=2,OB=
12+
|
(2-1)2+
|
∴OA=OB=AB,
所以△OAB是等边三角形.
故答案是:a=
| 3 |
(2)∵点C到△OAB各个顶点的距离相等,
∴点C是△OAB的外心,
∴C(1,
| ||
| 3 |
∵B(1,
| 3 |
∴BC=
2
| ||
| 3 |
在直角△OAD中,OA=2,∠OAD=30°,
∴OD=
2
| ||
| 3 |
所以四边形OCBD是平行四边形.
SOCBD=OD×1=
2
| ||
| 3 |
因此OCBD的面积为
2
| ||
| 3 |
(3)当点P(
| 2 |
| 3 |
2
| ||
| 9 |
| 2 |
| 3 |
4
| ||
| 9 |
当点P(
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
∴P1(
| 2 |
| 3 |
| 2 |
| 9 |
| 3 |
| ||
| 3 |
| ||
| 3 |
点评:本题考查的是抛物线的综合题,(1)把点的坐标代入抛物线,求出字母系数a的值,求三角形三边的长确定三角形的形状.(2)根据点C是三角形的外心,判断四边形OCBD是平行四边形,然后求出平行四边形的面积.(3)根据特殊梯形写出点P的坐标.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 |4-b|=0
|4-b|=0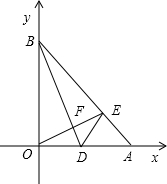
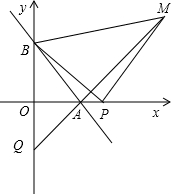
 (2013•长宁区二模)如图,直线AB交x轴于点A,交y轴于点B,O是坐标原点,A(-3,0)且sin∠ABO=
(2013•长宁区二模)如图,直线AB交x轴于点A,交y轴于点B,O是坐标原点,A(-3,0)且sin∠ABO=