Question

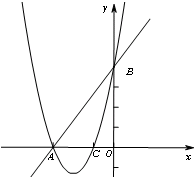（2013•长宁区二模）如图，直线AB交x轴于点A，交y轴于点B，O是坐标原点，A（-3，0）且sin∠ABO=

3

5

，抛物线y=ax²+bx+c经过A、B、C三点，C（-1，0）．
（1）求直线AB和抛物线的解析式；
（2）若点D（2，0），在直线AB上有点P，使得△ABO和△ADP相似，求出点P的坐标；
（3）在（2）的条件下，以A为圆心，AP长为半径画⊙A，再以D为圆心，DO长为半径画⊙D，判断⊙A和⊙D的位置关系，并说明理由．

Answer 1

分析：（1）根据sin∠ABO的值求出AB、OB的长度，从而得出点B的坐标，利用待定系数法可求出直线AB的解析式及抛物线解析式；
（2）根据（1）求出的直线AB的解析式，可设点P的坐标为（x，

4

3

x+4），①△ABO∽△APD，②△ABO∽△ADP，利用对应边成比例求出点P的坐标；
（3）根据（2）的答案，求出每种情况下的圆心距，继而可判断⊙A和⊙D的位置关系．

解答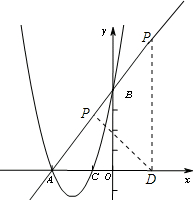：解：（1）在Rt△ABO中 sin∠ABO=

OA

AB

=

3

5

，
∵OA=3，
∴AB=5
则OB=

AB2-OA2

=4，
故点B的坐标为：（0，4），
设直线AB解析式为：y=kx+b（k≠0），
将A（-3，0）、B（0，4）代入得

-3k+b=0 b=4

，
解得：

k= 4 3 b=4

，
∴AB直线解析式：y=

4

3

x+4．
将A（-3，0）、C（-1，0）、B（0，4）代入抛物线解析式可得：

9a-3b+c=0 a-b+c=0 c=4

，
解得：

a= 4 3 b= 16 3 c=4

，
故抛物线解析式：y=

4

3

x²+

16

3

x+4．

（2）设P（x，

4

3

x+4），已知D的坐标为：（2，0），
①若△ABO∽△APD，
则

AO

AD

=

AB

AP

=

BO

PD

，即

3

5

=

4

DP

，
解得：DP=

20

3

，
故点P的坐标为（2，

20

3

）．
②若△ABO∽△ADP，
则

AB

AD

=

AO

AP

，即

5

5

=

3

AP

，
解得：AP=3，
则（x+3）²+（

4

3

x+4）²=3²，
解得：x₁=-

6

5

，x₂=-

24

5

（不符合题意，舍去），
故点P的坐标为：（-

6

5

，

12

5

）．
（3）⊙D的半径r=2，
当点P的坐标为（2，

20

3

）时，⊙A的半径AP=

25

3

，AD=5＜

25

3

-2，
故此时两圆内含；
当点P的坐标为：（-

6

5

，

12

5

）时，⊙A的半径AP=3，AD=5=3+2，
故此时两圆外切．

点评：本题考查了二次函数综合题，涉及了待定系数法求函数解析式，第二问需要分类讨论，不要漏解，第三问要求同学们掌握判断圆与圆位置关系的方法，有一定难度．