题目内容
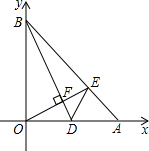
如图,直线AB交x轴正半轴于点A(a,0),交y轴正半轴于点B(0,b),且a、b满足| a-4 |
 |4-b|=0
|4-b|=0(1)求A、B两点的坐标;
(2)D为OA的中点,连接BD,过点O作OE⊥BD于F,交AB于E,求证:∠BDO=∠EDA.
分析:(1)由算是平方根结果大于等于0,绝对值结果大于等于0,又两者的和为0,可得两式同时为0,进而求出a与b的值,确定出A与B的坐标即可;
(2)要得到∠BDO=∠EDA,需证明△GDO≌△EDA,接下来找全等条件,过O作OG平分∠AOB,与BD交于点G,由∠AOB为直角,可得∠AOG等于直角的一半为45°,又三角形AOB为等腰直角三角形,可得∠BAO也为45°,故∠AOG=∠BAO,由D为OA的中点可得OD=AD,还差一个条件,利用△BOG≌△OAE可得OG=AE,这两个三角形全等的方法为:OA=OB,∠OBD与∠ODB互余,∠AOE与∠ODB也互余,故∠OBG=∠AOE,又OG平分∠AOB可得∠BOG=∠BAO=45°,利用ASA可得△BOG≌△OAE,得证.
(2)要得到∠BDO=∠EDA,需证明△GDO≌△EDA,接下来找全等条件,过O作OG平分∠AOB,与BD交于点G,由∠AOB为直角,可得∠AOG等于直角的一半为45°,又三角形AOB为等腰直角三角形,可得∠BAO也为45°,故∠AOG=∠BAO,由D为OA的中点可得OD=AD,还差一个条件,利用△BOG≌△OAE可得OG=AE,这两个三角形全等的方法为:OA=OB,∠OBD与∠ODB互余,∠AOE与∠ODB也互余,故∠OBG=∠AOE,又OG平分∠AOB可得∠BOG=∠BAO=45°,利用ASA可得△BOG≌△OAE,得证.
解答:(1)解:∵
≥0,|4-b|≥0,且
+|4-b|=0,
∴
=0,且|4-b|=0,即a-4=0,且4-b=0,
解得a=4,b=4,
则A(4,0),B(0,4);
(2)证明:作∠AOB的角平分线,交BD于点G,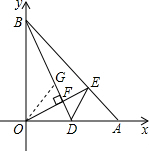
∵∠AOB=90°,OA=OB,
∴∠BOG=∠OAE=45°,
∵OB=OA,
∴∠OAB=∠OBA=45°,
∴∠GOD=∠EAD=45°,
∵∠OBG+∠ODB=90°,∠AOE+∠ODB=90°,
∴∠OBG=∠AOE,
在△BOG和△OAE中,
,
∴△BOG≌△OAE(ASA),
∴OG=AE,
又D为OA的中点,得到OD=AD,
在△GDO和△EDA中,
,
∴△GDO≌△EDA(SAS)
∴∠BDO=∠EDA.
| a-4 |
| a-4 |
∴
| a-4 |
解得a=4,b=4,
则A(4,0),B(0,4);
(2)证明:作∠AOB的角平分线,交BD于点G,

∵∠AOB=90°,OA=OB,
∴∠BOG=∠OAE=45°,
∵OB=OA,
∴∠OAB=∠OBA=45°,
∴∠GOD=∠EAD=45°,
∵∠OBG+∠ODB=90°,∠AOE+∠ODB=90°,
∴∠OBG=∠AOE,
在△BOG和△OAE中,
|
∴△BOG≌△OAE(ASA),
∴OG=AE,
又D为OA的中点,得到OD=AD,
在△GDO和△EDA中,
|
∴△GDO≌△EDA(SAS)
∴∠BDO=∠EDA.
点评:此题考查了全等三角形的判定与性质,等腰直角三角形的性质,非负数(绝对值及算术平方根)的性质,以及坐标与图形的性质,要求学生掌握两非负数相加为0时其两加数同时为0,第二问证明时利用两次全等的方法得到的,学生做题时注意挖掘题中的隐含条件,比如x轴于y轴夹角为直角,还可利用同角的余角相等及等量代换充分利用已知条件找证明全等三角形的条件,全等三角形的判定方法有:SSS;SAS;ASA;AAS;HL(直角三角形).其中作出辅助线OG平分∠AOB是第二问的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 各顶点的距离相等,直线AC交y轴于点D.
各顶点的距离相等,直线AC交y轴于点D.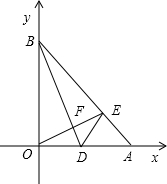
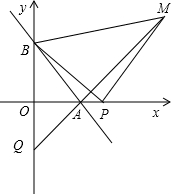
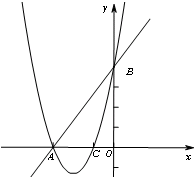 (2013•长宁区二模)如图,直线AB交x轴于点A,交y轴于点B,O是坐标原点,A(-3,0)且sin∠ABO=
(2013•长宁区二模)如图,直线AB交x轴于点A,交y轴于点B,O是坐标原点,A(-3,0)且sin∠ABO=