题目内容
(2011•盘锦)如图,风车的支杆OE垂直于桌面,风车中心O到桌面的距离OE为25cm,小小风车在风吹动下绕着中心O不停地转动,转动过程中,叶片端点A、B、C、D在同一圆O上,已知⊙O的半径为10cm.
(1)风车在转动过程中,当∠AOE=45°时,求点A到桌面的距离(结果保留根号).
(2)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm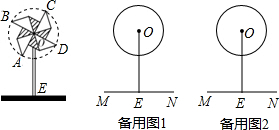 所经过的路径长(结果保留π).
所经过的路径长(结果保留π).
(1)风车在转动过程中,当∠AOE=45°时,求点A到桌面的距离(结果保留根号).
(2)在风车转动一周的过程中,求点A相对于桌面的高度不超过20cm
 所经过的路径长(结果保留π).
所经过的路径长(结果保留π).分析:(1)作A1F⊥MN于点F,A1G⊥OE于点G,在Rt△A1OG中,利用三角函数可求得OG,从而得出点A到桌面的距离A1F;
(2)作A2H⊥MN于H,则A2H=20.作A2D⊥OE于点D,则DE=A2H.在Rt△A2OD中,由特殊角的三角函数得∠A2OD=60°,由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°.从而得出点A所经过的路径长.
(2)作A2H⊥MN于H,则A2H=20.作A2D⊥OE于点D,则DE=A2H.在Rt△A2OD中,由特殊角的三角函数得∠A2OD=60°,由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°.从而得出点A所经过的路径长.
解答: 解:(1)如图(1),点A运动到点A1的位置时∠AOE=45°.
解:(1)如图(1),点A运动到点A1的位置时∠AOE=45°.
作A1F⊥MN于点F,A1G⊥OE于点G,
∴A1F=GE.(1分)
在Rt△A1OG中,
∵∠A1OG=45°,OA1=10,
∴OG=OA1•cos45°=10×
=5
.(2分)
∵OE=25,
∴GE=OE-OG=25-5
.
∴A1F=GE=25-5
.(3分)
答:点A到桌面的距离是(25-5
)厘米.(4分)
(2)如图(2),点A在旋转过程中运动到点A2、A3的位置时,点A到桌面的距离等于20厘米.
作A2H⊥MN于H,则A2H=20.作A2D⊥OE于点D,
∴DE=A2H.(5分)
∵OE=25,
∴OD=OE-DE=25-20=5.
在Rt△A2OD中,
∵OA2=10,
∴cos∠A2OD=
=
=
.
∴∠A2OD=60°.(7分)
由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°.
∴点A所经过的路径长为
=
.(9分)
答:点A所经过的路径长为
厘米.(10分)
 解:(1)如图(1),点A运动到点A1的位置时∠AOE=45°.
解:(1)如图(1),点A运动到点A1的位置时∠AOE=45°.作A1F⊥MN于点F,A1G⊥OE于点G,
∴A1F=GE.(1分)
在Rt△A1OG中,
∵∠A1OG=45°,OA1=10,
∴OG=OA1•cos45°=10×
| ||
| 2 |
| 2 |
∵OE=25,
∴GE=OE-OG=25-5
| 2 |
∴A1F=GE=25-5
| 2 |
答:点A到桌面的距离是(25-5
| 2 |
(2)如图(2),点A在旋转过程中运动到点A2、A3的位置时,点A到桌面的距离等于20厘米.

作A2H⊥MN于H,则A2H=20.作A2D⊥OE于点D,
∴DE=A2H.(5分)
∵OE=25,
∴OD=OE-DE=25-20=5.
在Rt△A2OD中,
∵OA2=10,
∴cos∠A2OD=
| OD |
| OA2 |
| 5 |
| 10 |
| 1 |
| 2 |
∴∠A2OD=60°.(7分)
由圆的轴对称性可知,∠A3OA2=2∠A2OD=120°.
∴点A所经过的路径长为
| 120π×10 |
| 180 |
| 20π |
| 3 |
答:点A所经过的路径长为
| 20π |
| 3 |
点评:本题考查了弧长的计算、勾股定理、特殊角的三角函数值以及锐角三角函数的定义,综合性较强难度偏大.

练习册系列答案
相关题目
 线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.
线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米. (2011•盘锦)如图,已知⊙O的半径为4,点D是直径AB延长线上一点,DC切⊙O于点C,连接AC,若∠CAB=30°,则BD的长为( )
(2011•盘锦)如图,已知⊙O的半径为4,点D是直径AB延长线上一点,DC切⊙O于点C,连接AC,若∠CAB=30°,则BD的长为( ) (2011•盘锦)如图,矩形纸片ABCD,AD=2AB=4,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则DE=
(2011•盘锦)如图,矩形纸片ABCD,AD=2AB=4,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则DE=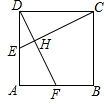 (2011•盘锦)如图,在正方形ABCD中,点E、F分别为AD、AB的中点,连接DF、CE,DF与CE交于点H,则下列结论:①DF⊥CE;②DF=CE;③
(2011•盘锦)如图,在正方形ABCD中,点E、F分别为AD、AB的中点,连接DF、CE,DF与CE交于点H,则下列结论:①DF⊥CE;②DF=CE;③