题目内容
(2011•盘锦)如图,直线y=
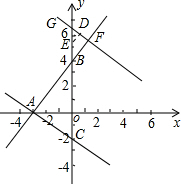
x+m(m≠0)交x轴负半轴于点A、交y轴正半轴于点B且AB=5,过点A作直线AC⊥AB交y轴于点C.点E从坐标原点O出发,以0.8个单位/秒的速度沿y轴向上运动;与此同时直线l从与直线AC重合的位置出发,以1个单位/秒的速度沿射线AB方向平行移动.直线l在平移过程中交射线AB于点F、交y轴于点G.设点E离开坐标原点O的时间为t(t≥0)s.
(1)求直线AC的解析式;
(2)直线l在平移过程中,请直接写出△BOF为等腰三角形时点F的坐标;
(3)直线l在平移过程中,设点E到直线l的距离为d,求d与t的函数关系.

| m | 3 |
(1)求直线AC的解析式;
(2)直线l在平移过程中,请直接写出△BOF为等腰三角形时点F的坐标;
(3)直线l在平移过程中,设点E到直线l的距离为d,求d与t的函数关系.

分析:(1)根据已知条件表示出A、B的坐标,再根据AB=5得出m的值,即可求出OB的值,再根据直线AC⊥AB交y轴于点C,得出△BOA∽△AOC,从而得出CO的值,再根据点C在y轴负半轴上,得出C点的坐标,然后设直线AC解析式为y=kx+b,把A,C点代入求出解析式;
(2)根据(1)的证明直接得出△BOF为等腰三角形时点F的坐标;
(3)先分两种情况进行讨论:当0≤t≤5时,先作ED⊥FG于D,得出ED=d,得出FG∥AC,再根据AF=t,AB=5得出BF的值,即可求出BC的值,再根据BC的值求出BG的值,再根据FG⊥AB,ED⊥FG,得出∠GDE=∠GFB=90°,求出ED∥AB,即可求出d与t的函数关系;再求当t>5时,先作ED⊥FG于D,得出ED=d,得出FG∥AC,得出B点的坐标,求出BC的值,从而得出BE,EG的值,再根据FG⊥AB,ED⊥FG,∠GDE=∠GFB=90°,得出ED∥AB即可求出d与t的函数关系;
(2)根据(1)的证明直接得出△BOF为等腰三角形时点F的坐标;
(3)先分两种情况进行讨论:当0≤t≤5时,先作ED⊥FG于D,得出ED=d,得出FG∥AC,再根据AF=t,AB=5得出BF的值,即可求出BC的值,再根据BC的值求出BG的值,再根据FG⊥AB,ED⊥FG,得出∠GDE=∠GFB=90°,求出ED∥AB,即可求出d与t的函数关系;再求当t>5时,先作ED⊥FG于D,得出ED=d,得出FG∥AC,得出B点的坐标,求出BC的值,从而得出BE,EG的值,再根据FG⊥AB,ED⊥FG,∠GDE=∠GFB=90°,得出ED∥AB即可求出d与t的函数关系;
解答:解:(1)∵y=
x+m交x轴负半轴于点A、交y轴正半轴于点B,
∴B(0,m)、A(-3,0).
∵AB=5,
∴m2+32=52,
解得m=±4.
∵m>0,
∴m=4.
∴B(0,4).
∴OB=4.
∵直线AC⊥AB交y轴于点C,易得△BOA∽△AOC,
∴
=
.
∴CO=
=
=
.
∵点C在y轴负半轴上,
∴C(0,-
).
设直线AC解析式为y=kx+b,
∵A(-3,0),C(0,-
),
∴
,
解得
,
∴y=-
x-
;
(2)F1(
,
)、F2(-
,
)、F3.(-
,2);
(3)分两种情况:第一种情况:当0≤t≤5时,
如图,作ED⊥FG于D,则ED=d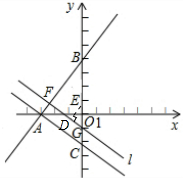 .
.
由题意,FG∥AC,
∴
=
,
∵AF=t,AB=5,
∴BF=5-t.
∵B(0,4),
∴BC=4+
=
.
∴
=
.
∴BG=
(5-t).
∵OE=0.8t,OB=4,
∴BE=4-0.8t.
∴EG=
(5-t)-(4-0.8t)=
-
t.
∵FG⊥AB,ED⊥FG,
∴∠GDE=∠GFB=90°.
∴ED∥AB.
∴
=
.
∴
=
.
∴d=-
t+
.
第二种情况:当t>5时,
如图(2),
作ED⊥FG于D,则ED=d,
则题意,FG∥AC,
∴
=
.
∵AF=t,AB=5,
∴BF=t-5.
∵B(0,4),C(0,-
),
∴BC=4+
=
.
∴
=
.
 ∴BG=
∴BG=
(t-5).
∵OE=0.8t,OB=4,
∴BE=0.8t-4,EG=
(t-5)-(0.8t-4),
=
t-
.
∵FG⊥AB,ED⊥FG,∠GDE=∠GFB=90°,
∴ED∥AB.
∴
=
.
∴
=
.
∴d=
t-
.
| m |
| 3 |
∴B(0,m)、A(-3,0).
∵AB=5,
∴m2+32=52,
解得m=±4.
∵m>0,
∴m=4.
∴B(0,4).
∴OB=4.
∵直线AC⊥AB交y轴于点C,易得△BOA∽△AOC,
∴
| AO |
| BO |
| CO |
| AO |
∴CO=
| AO2 |
| BO |
| 32 |
| 4 |
| 9 |
| 4 |
∵点C在y轴负半轴上,
∴C(0,-
| 9 |
| 4 |
设直线AC解析式为y=kx+b,
∵A(-3,0),C(0,-
| 9 |
| 4 |
∴
|
解得
|
∴y=-
| 3 |
| 4 |
| 9 |
| 4 |
(2)F1(
| 12 |
| 5 |
| 36 |
| 5 |
| 12 |
| 5 |
| 4 |
| 5 |
| 3 |
| 2 |
(3)分两种情况:第一种情况:当0≤t≤5时,
如图,作ED⊥FG于D,则ED=d
 .
.由题意,FG∥AC,
∴
| BF |
| BA |
| BG |
| BC |
∵AF=t,AB=5,
∴BF=5-t.
∵B(0,4),
∴BC=4+
| 9 |
| 4 |
| 25 |
| 4 |
∴
| 5-t |
| 5 |
| BG | ||
|
∴BG=
| 5 |
| 4 |
∵OE=0.8t,OB=4,
∴BE=4-0.8t.
∴EG=
| 5 |
| 4 |
| 9 |
| 4 |
| 9 |
| 20 |
∵FG⊥AB,ED⊥FG,
∴∠GDE=∠GFB=90°.
∴ED∥AB.
∴
| EG |
| BG |
| ED |
| BF |
∴
| ||||
|
| d |
| 5-t |
∴d=-
| 9 |
| 25 |
| 9 |
| 5 |
第二种情况:当t>5时,
如图(2),
作ED⊥FG于D,则ED=d,
则题意,FG∥AC,
∴
| BF |
| BA |
| BG |
| BC |
∵AF=t,AB=5,
∴BF=t-5.
∵B(0,4),C(0,-
| 9 |
| 4 |
∴BC=4+
| 9 |
| 4 |
| 25 |
| 4 |
∴
| t-5 |
| 5 |
| BG | ||
|
 ∴BG=
∴BG=| 5 |
| 4 |
∵OE=0.8t,OB=4,
∴BE=0.8t-4,EG=
| 5 |
| 4 |
=
| 9 |
| 20 |
| 9 |
| 4 |
∵FG⊥AB,ED⊥FG,∠GDE=∠GFB=90°,
∴ED∥AB.
∴
| EG |
| BG |
| ED |
| BF |
∴
| ||||
|
| d |
| t-5 |
∴d=
| 9 |
| 25 |
| 9 |
| 5 |
点评:此题考查了一次函数的综合;解题的关键是求出各点的坐标,再用各点的坐标求出解析式,注意(3)中分两种情况进行讨论,不要漏掉.

练习册系列答案
相关题目
 线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米.
线BD上.若AB=6m,AD=4m,设AM的长为xm,矩形AMPQ的面积为S平方米. (2011•盘锦)如图,已知⊙O的半径为4,点D是直径AB延长线上一点,DC切⊙O于点C,连接AC,若∠CAB=30°,则BD的长为( )
(2011•盘锦)如图,已知⊙O的半径为4,点D是直径AB延长线上一点,DC切⊙O于点C,连接AC,若∠CAB=30°,则BD的长为( ) (2011•盘锦)如图,矩形纸片ABCD,AD=2AB=4,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则DE=
(2011•盘锦)如图,矩形纸片ABCD,AD=2AB=4,将纸片折叠,使点C落在AD上的点E处,折痕为BF,则DE=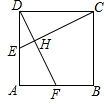 (2011•盘锦)如图,在正方形ABCD中,点E、F分别为AD、AB的中点,连接DF、CE,DF与CE交于点H,则下列结论:①DF⊥CE;②DF=CE;③
(2011•盘锦)如图,在正方形ABCD中,点E、F分别为AD、AB的中点,连接DF、CE,DF与CE交于点H,则下列结论:①DF⊥CE;②DF=CE;③