题目内容
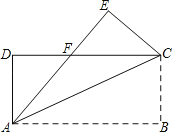
【题目】如图,长方形ABCD中,AB=8cm,AD=4cm,将△ABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点.
(1)试说明AF=CF;
(2)求DF的长.
【答案】(1)证明见解析(2)5cm
【解析】试题分析:(1)根据矩形的性质和折叠的性质,得到AD=CE,∠D=∠E,然后根据全等三角形的判定AAS,证得△ADF≌△CEF,从而得证结论;
(2)根据(1)的结论求出AF=CF,然后在直角三角形ADF中,设出相应的边长,根据勾股定理构造方程求解即可.
试题解析:(1)∵四边形ABCD是长方形,
∴∠D=90°,AD=BC,AB=DC=8cm,
∵将△ABC沿着对角线AC折叠,使点B落在E处,AE交CD于F点,
∴∠D=∠E=90°,CE=BC=AD,
在△ADF和△CEF中,
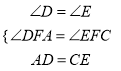
∴△ADF≌△CEF(AAS),
∴AF=CF;
(2)∵△ADF≌△CEF,
∴AF=CF,
设DF为xcm,则CF=AF=(8﹣x)cm,在直角△ADF中,由勾股定理得:
x2+42=(8﹣x)2,
解得:x=3,
CF=AF=3cm,
则DF=8cm﹣3cm=5cm.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
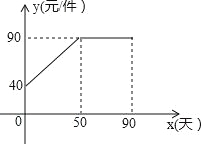
【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.