题目内容
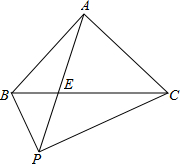 如图,P为等腰Rt△ABC外一点,∠BAC=90°,连PB、PC、PA,PA交BC于E点,且∠APC=45°,下列结论:
如图,P为等腰Rt△ABC外一点,∠BAC=90°,连PB、PC、PA,PA交BC于E点,且∠APC=45°,下列结论:
①∠BPA=45°.②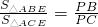 .③PB+PC=
.③PB+PC= PA.
PA.
其中正确的是
- A.①
- B.①②
- C.②
- D.①②③
D
分析:求出∠ABC=∠APC,即推出A、B、P、C四点共圆,根据圆内接四边形的对角互补即可求出∠APB的度数;求出△BAE∽△PAB,推出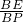 =
=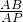 ,证△CAE∽△PAC,推出
,证△CAE∽△PAC,推出 =
= ,推出
,推出 =
= ,根据三角形的面积公式即可求出②正确;过A作AD⊥PA,AD交PB的延长线于D,证△ADB≌△APC,推出PC=BD,AD=AP,得出△DAP是等腰直角三角形,由勾股定理求出DP=
,根据三角形的面积公式即可求出②正确;过A作AD⊥PA,AD交PB的延长线于D,证△ADB≌△APC,推出PC=BD,AD=AP,得出△DAP是等腰直角三角形,由勾股定理求出DP= AP,即可推出③正确.
AP,即可推出③正确.
解答: ∵△ABC是等腰直角三角形,
∵△ABC是等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵∠APC=45°,
∴∠ABC=∠APC,
即A、B、P、C四点共圆,
∴∠APB=∠ACB=45°,
∴①正确;
∵∠APB=∠ABC=45°,∠BAE=∠PAB,
∴△BAE∽△PAB,
∴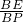 =
=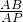 ,
,
同理可证△CAE∽△PAC,
∴ =
= ,
,
∵AB=AC,
∴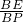 =
= ,
,
即 =
= ,
,
∵△ABE的边BE上的高和△ACE的边CE上的高相同,设高为h,
∴ =
= =
= =
=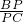 ,
,
∴②正确;
过A作AD⊥PA,AD交PB的延长线于D,
∵∠BAC=90°,AD⊥PA,
∴∠DAP=90°=∠BAC,
∴∠1+∠2=∠2+∠3,
∴∠1=∠3,
∵A、B、P、C四点共圆,
∴∠4=∠ACP,
在△ADB和△APC中
 ,
,
∴△ADB≌△APC(ASA),
∴PC=BD,AD=AP,
∴△DAP是等腰直角三角形,
由勾股定理得:DP= =
= AP,
AP,
∵DP=BP+BD=BP+PC,
即PB+PC= PA,
PA,
∴③正确;
故选D.
点评:本题考查了圆内接四边形,相似三角形的性质和判定,全等三角形的性质和判定,三角形的内角和定理,等腰直角三角形等知识点的综合运用,题目综合性比较强,难度偏大.
分析:求出∠ABC=∠APC,即推出A、B、P、C四点共圆,根据圆内接四边形的对角互补即可求出∠APB的度数;求出△BAE∽△PAB,推出
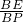 =
=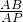 ,证△CAE∽△PAC,推出
,证△CAE∽△PAC,推出 =
= ,推出
,推出 =
= ,根据三角形的面积公式即可求出②正确;过A作AD⊥PA,AD交PB的延长线于D,证△ADB≌△APC,推出PC=BD,AD=AP,得出△DAP是等腰直角三角形,由勾股定理求出DP=
,根据三角形的面积公式即可求出②正确;过A作AD⊥PA,AD交PB的延长线于D,证△ADB≌△APC,推出PC=BD,AD=AP,得出△DAP是等腰直角三角形,由勾股定理求出DP= AP,即可推出③正确.
AP,即可推出③正确.解答:
 ∵△ABC是等腰直角三角形,
∵△ABC是等腰直角三角形,∴∠ABC=∠ACB=45°,
∵∠APC=45°,
∴∠ABC=∠APC,
即A、B、P、C四点共圆,
∴∠APB=∠ACB=45°,
∴①正确;
∵∠APB=∠ABC=45°,∠BAE=∠PAB,
∴△BAE∽△PAB,
∴
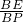 =
=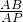 ,
,同理可证△CAE∽△PAC,
∴
 =
= ,
,∵AB=AC,
∴
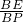 =
= ,
,即
 =
= ,
,∵△ABE的边BE上的高和△ACE的边CE上的高相同,设高为h,
∴
 =
= =
= =
=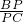 ,
,∴②正确;

过A作AD⊥PA,AD交PB的延长线于D,
∵∠BAC=90°,AD⊥PA,
∴∠DAP=90°=∠BAC,
∴∠1+∠2=∠2+∠3,
∴∠1=∠3,
∵A、B、P、C四点共圆,
∴∠4=∠ACP,
在△ADB和△APC中
 ,
,∴△ADB≌△APC(ASA),
∴PC=BD,AD=AP,
∴△DAP是等腰直角三角形,
由勾股定理得:DP=
 =
= AP,
AP,∵DP=BP+BD=BP+PC,
即PB+PC=
 PA,
PA,∴③正确;
故选D.
点评:本题考查了圆内接四边形,相似三角形的性质和判定,全等三角形的性质和判定,三角形的内角和定理,等腰直角三角形等知识点的综合运用,题目综合性比较强,难度偏大.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 12、如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①DE=DG;②BE=CG;③DF=DH;④BH=CF.其中正确的是( )
12、如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①DE=DG;②BE=CG;③DF=DH;④BH=CF.其中正确的是( ) 18、如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①DE=DG,②BE=CG,③DF=DH,④BH=CF.其中正确地是
18、如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①DE=DG,②BE=CG,③DF=DH,④BH=CF.其中正确地是 如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①DE=DG,②BE=CG,③DF=DH,④BH=CF.其中正确的是________.
如图,D为等腰Rt△ABC的斜边AB的中点,E为BC边上一点,连接ED并延长交CA的延长线于点F,过D作DH⊥EF交AC于G,交BC的延长线于H,则以下结论:①DE=DG,②BE=CG,③DF=DH,④BH=CF.其中正确的是________.